Recovery System Design

DESIGN OF A PARACHUTE RECOVERY AND LANDING SYSTEM

This chapter deals with the design of a parachute recovery and landing attenuation system for a military reconnaissance drone. The prime emphasis in the design of this system is on undamaged recovery of the drone from the total flight performance envelope during the development and test phase, on undamaged recovery after a completed mission during military operations, and on multiple use of the recovery system. An engineering team conducts performance and system analyses and chooses what recovery concept to use, what types of parachutes to select for high-speed deceleration and for final recovery, and what impact-attenuation system is best for the particular application. This chapter covers the selection process for concepts and components. Different engineers may make different selections based on experiences with particular types of parachutes or deployment concepts; experience is always a viable reason for selecting a particular approach. However, using the selection criteria shown in Figure 2-6. the designer must put reliability of operation, undamaged recovery, reusability of the landing system, and minimum weight and volume at the top of the list of requirements.

7.1 REQUIREMENTS

7.1.1 System Requirements

An unmanned air vehicle used for military reconnaissance must be recovered after a completed mission in rough terrain, undamaged and ready for multiple reuses. The recovery system must be able to

1. Recover the air vehicle after the completed mission when the vehicle has landed in rough terrain at altitudes from sea level to 5000 feet.
2. Recover the drone during the engineering test phase from all controlled and uncontrolled flight conditions.
3. Serve as a range-safety device to prevent the air vehicle from leaving the boundaries of the test range.

The air vehicle has a takeoff weight of 7200 pounds and a landing weight, after the completed mission, of 4800 pounds. Undamaged landing shall be possible in rough terrain with rocks up to 8 inches in diameter. Replacement parts and refurbishment cost shall be kept to a minimum.

7.1.2 Requirements for Normal Operation

Drone weight at recovery after completed mission	Wd = 4800 lb
Recovery velocity	vo = 150 to 200 KEAS
Minimum recovery altitude	Ho = 2000 ft above ground level (AGL)
Maximum ground level	H = 5000 ft
Maximum allowable total parachute force	Fo = 16,000 lb
Maximum allowable impact deceleration at landing	a = 9.0 g's

7.1.3 Requirements for Emergency Operation

Emergency operation includes recovery during the test phase from takeoff to landing and also includes recovery for range-safety reasons.

Drone weight at takeoff	Wdmax = 7200 lb
Maximum recovery velocity at mean sea level (MSL)	vo = 490 KEAS
Maximum recovery velocity at 38,000 to 50,000 ft altitude	vo = 1.5 Mach
Maximum dynamic pressure	qmax = 812 lb/ft2
Maximum allowable parachute force	Fo = 22,000 lb

7.1.4 Requirements Analysis

Three primary requirements pace the design of the recovery system:

1. The drone must be able to land in rocky but level terrain without damage.
2. Refurbishment cost and time shall be kept to a minimum.
3. Recovery must be possible from all flight conditions during the flight test phase, including cases where the out-of-control drone flies off the range.

7.2 LANDING ANALYSIS AND IMPACT-ATTENUATION SYSTEM

7.2.1 Landing Analysis

Three known recovery concepts prevent damage during landing in rocky terrain:

1. Midair retrieval.
2. Dual air bags or dual frangibles.
3. Retrorockets combined with small, nondeflatable air bags.

The need for retrieval helicopters or retrieval aircraft makes Method 1, midair retrieval, impractical. The other two methods are affected by the deceleration distance required to meet the 9-g limit.

In section 6.8 of this manual, the required deceleration distance(s) is determined to be

$s={\frac {{V_{e_{1}}}^{2}-{V_{e_{2}}}^{2}}{2g(n\eta -1)}}$

where

${V_{e_{1}}}$ = velocity of the drone descending on the parachute (rate of descent), ft/s

$V_{e_{2}}$ = permissible impact velocity, ft/s

$g$ = acceleration of gravity, ft/s2

$\eta$ = effectiveness of the impact attenuation system used, dimensionless

$n$ = allowable impact deceleration, ratio $n={\frac {a}{g}}$

Figure 6-68 of Chapter 6 shows the range of various impact attenuation systems as a function of rate of descent and allowable ground impact deceleration. The information indicates that air bags may be the most practical concept for this application. A cursory analysis indicates that a rate of descent of 25 ft/s at 5000 feet: altitude will result in a close to optimum weight ratio of the combined parachute air bag system (see Figure 6-83). Properly designed air bags will have an effectiveness of 65% as shown in the stroke-pressure diagram in Figure 6-78 and allow ground contact or final velocity of close to 0 ft/s.

With these assumptions, the required effective air bag deceleration stroke is obtained.

$s={\frac {25^{2}-00}{(2\cdot 32.174)(9.0\cdot 0.65-1)}}=2.0\ ft\ or\ 24\ in.$

This deceleration distance is too short for a parachute retrorocket system because of the required timing accuracy and rocket burning time. Retrorocket systems are most practical for deceleration distances greater than 4 or 5 feet. Crushable and frangible impact attenuators are suitable for deceleration distances of less than 15 inches. Air bag systems work best for deceleration distances of 24 to 48 inches. The original assumption that an air bag concept maybe the most practical approach for this air vehicle is therefore confirmed.

7.2.2 Impact Attenuator System

The design of impact attenuator systems is discussed in section 6.8 of this manual. Figure 7-1 shows the reconnaissance drone and the air-bag attenuator systems that consist of two deflatable, two-compartment wing-bag bags (A); a single-compartment, deflatable nose bag (B); and a nondeflatable nose-buffer bag (C). The wing bags, the primary energy absorbers, need the already calculated 24-inch effective-deceleration stroke. For design reasons, 33 inches must be added to the bag height, 19 inches for the distance from the wing underside to the underside of the jet airducts, 10 inches for ground clearance, and 4 inches for bag bottom curvature. These additions result in a total bag height of 57 inches. To ensure landing stability, an air bag height-to-diameter ratio of 1.25 is selected for the two wing bags, resulting in a bag diameter of 48 inches. The cross-hatched lower part of the two wing bags (see Figure 7-1) deflates at impact, but the upper part stays inflated and keeps the drone off the ground. The nose bag, B, helps to absorb the impact and deflates, and the nose of the drone comes to rest on the nondeflatable buffer bag, C. All air bags are inflated from 3000 psi nitrogen containers using aspirators for a 50/50 nitrogen air mixture. The air bags are prepressurized to 2 psi for full bag inflation prior to landing. Multiple blowout valves consisting of staggered blowout rubber disks around the circumference of the air bags control the bag deflation to stay within the 9-g deceleration limit.

The weight of the impact-attenuation system-air bags, nitrogen containers, plumbing, and A/C containers-is estimated from section 6.7 to be 2.2% of the total drone weight, or 105.6 pounds. The air bags should be stored in containers that can be easily removed from the drone for repacking. Air bags must be deployed after the main parachutes are fully open to prevent air-bag damage caused by high dynamic pressure. Air-bag deployment begins with simultaneous pyroejecting of the removable air-bag-container covers and opening of the nitrogen-container valves. The wing bags, the primary nose bag, and the nose-buffer bag inflate. At ground contact, the bags compress, increasing the pressure inside the bags. At a preselected pressure level, the blowout valves (rubber disks, metal disks, or rubber-type sleeves) open and limit the maximum drone deceleration to the preselected level.

FIGURE 7-1. Reconnaissance-Drone and Air Bag Configurations.

$deceleration\ a={\frac {bag\ pressure\cdot bag\ ground\ contact\ area}{drone\ weight,W_{d}}}$

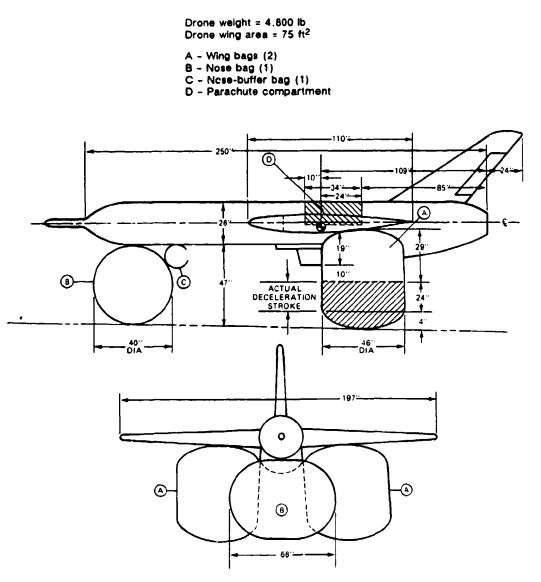
The drone comes to rest on the upper compartment of the two wing bags and the nose-buffer bag.

The pressure increases in the bags at ground contact, in connection with a short time delay (0.5 to 1.0), may be used as a signal for disconnecting the main parachutes to prevent wind-dragging of the drone.

7.3 MAIN PARACHUTE SYSTEM

7.3.1 Main Parachute System Requirements

Weight to be recovered:

Operational	Wd = 4800 lb
Test phase	Wd max = 7200 lb
Recovery velocity	vo = 150 to 200 KEAS
Recovery altitude	Ho = 2000 ft AGL
Maximum ground level	H = 5000 ft
Rate of descent	ve = 25 ft/s at 5000 ft
Stability	Oscillation of not more than ± 5 deg
Maximum total parachute force	F ≤ 16,000 lb = 3.3 g

Maximum recovery-system weight and volume are prime requirements.

7.3.2 Parachute Assembly Section

Section 2.4 defines the criteria for parachute type selection. Requirements for low weight and volume rule out the low-drag slotted parachutes (ribbon, ringslot, and ringsail) as well as guide-surface and cross parachutes (see Tables 5.2 and 5.3). Parachute deployment past the vertical stabilizer rules out a single parachute in favor of a cluster of two parachutes deployed independently left and right of the vertical stabilizer.

No cluster experience is available with annular or cross parachutes, and no reefing experience is available with annular parachutes. Cross parachutes cannot be reefed to the low reefing ratios required for this application. Extended-skirt and polyconical parachutes have been used successfully in clusters of large, reefed parachutes.

A cluster of two conical full extended skirt parachutes is most suitable for this system. In section 5.2, Figures 5-24 and 5-25 show that properly designed extended-skirt parachutes have drag coefficients equal to 0.8 to 0.9 in the 20- to 25-ft/s rate of descent range. Available data (Reference 5.23) indicate that a cluster of two extended-skirt parachutes is sufficiently stable for use with air bags. Extended-skirt parachutes have a low opening-force coefficient of 1.4, compared to an opening-force coefficient of 1.8 for conical and triconical parachutes. Extended-skirt parachutes can also be reefed to low reefing ratios, a requirement for final descent parachutes (see Chapter 5, Figure 5-72).

7.3.3 Parachute Diameter

The rate of descent at 5000 feet altitude was selected to 25 ft/s (see section 7.3.1). The

equivalent rate of descent at sea level is:

$Ve_{o}=V_{e}{\sqrt {\rho /\rho _{o}}}=25ft/s{\sqrt {\sigma }}$

${\sqrt {\sigma }}$ at 5000 ft is 0.9283 (see Table 3-3); therefore,

$V_{e}{_{o}}=25ft/s\ (0.9283)=23.2ft/s$

The required parachute drag area, $(C_{D}S)_{p}$ for one parachute is calculated

The drag coefficient, CDo, for a conical full extended skirt parachute with a 23.2-ft/s rate of

descent and a suspension-line ratio, [.e/Do, of 1.0 is obtained from Figure 5-25

A suspension-line ratio of 1.15 is selected. This is the longest practical length for extended skirt

parachutes (see Figure 5-20).

The length of the riser, Lr, depends on its installation in the drone; the riser should be long

enough to extend beyond the fuselage and vertical stabilizer of the drone (see Figure 7-2),

which gives the final configuration of the parachute cluster, including risers and parachutes.

7.3.4 Parachute Deployment System

A cluster of two main parachutes is selected and deployed left and right of the vertical

stabilizer to avoid hang-up or damage of a single parachute by the vertical stabilizer. Each

parachute needs its own extraction and deployment system to properly deploy past the

stabilizer and to avoid interference with the other main parachute during deployment and

inflation.

Two fast-opening extraction parachutes are used on each main parachute. Stable

parachutes will minimize interferenc, during deployment. Experience with past recovery

systems has shown that the most positive deployment is obtained by forced ejection of the

extractiou or pilot chutes into good airflow past the vertical stabilizer by either mortar or

drogue gun ejection. A mortar can eject large, heavy parachutes but creates large leaction

forces and needs considerable space for installation. Drogue gun ejection is effective, but is

limited to the deployment of small, lightweight parachutes such as pilot chutes. Drogue gun ejected pilot chutes are selected for initiating main parachute deployment. To ensure proper

clearance of the vertical stabilizer, the pilot chutes are ejeLted 45 degrees upward, backward

and outward past the vertical stabilizer. The parachute installation in the drone fuselage

requires cross-wind deployment and therefore forced ejection of the main parachute

deployment bags. Four different methods have been used successfully to accomplish forced

ejection: (1) using ejector springs enclosed in a textile cylinder. (2) gas-inflating nonporous

ejector bags, (3) catapulting the bag out of the compartment, or (4) using a lift-web

arrangement as discussed in section 6.1.

The deployment system selected consists of a drogue gun deployed pilot chute, an

extraction parachute, and a main parachute deployment bag lifted from the parachute

compartment by lift webs. When the hinged compartment doors open, two drogue gun slugs

are fired 45 degrees upward and aft; each slug deploys a pilot chute sufficiently behind the

drone into good airflow. These pilot chutes in turn extract two extraction chutes stowed on top of the main parachute deployment bags. The extraction chutes extract and deploy the two main 0

parachutes left and right of the vertical stabilizers. Lift webs and unsymmetrical bag handles

lift the main parachute bags out of the drone compartment and extract the main parachute

past the vertical stabilizer (see Figure 7-3)

7.3.5 Extraction Parachute Assembly

The two extraction parachutes must properly deploy the two main parachutes. The size of

the extraction parachutes and their location in the wake of the drone is determined as follows:

1. The ratio of the drag area of the extraction parachute, (CDS)EP, to the drag area of the

main parachutes, (CDS)Mp, has been evaluated for various deployment velocities (see

section 6.3, Table 6-5). For the 150- to 200-KEAS-velocity range, a (CDS)EP/(CDS)Mp ratio of

0.007 is selected.

2. The leading edge of the extraction parachute must be placed 6 forebody diameters

behind the drone to ensure good inflation in the wake of the forebody.

The size of the extraction parachute is determined to be

(COS)EP = 0.007 . 3744 ft 2 = 26.20 ft2

The forebody diameter of the noncylindrical drone fuselage, shown in Figure 7-4 and

discussed in section 5.2, is used to determine the location of the extraction parachute.

The equivalent forebody diameter is determined from the netted forebody area

SFB = 4.9 ft2 to

V4 F4

DFB SFB = 4.9 ft 2 = 30 in.

7-10

NWC TP 6575

Dp-INFLATED EXI RACTION

S CHUTE DIAMETER

SFB=FOREBODY WETTED AREA

FIGURE 7-4. Determination of Equivalent

Forebody Diameter.

The distance between the tail of the drone and the leading edge of the extraction parachute is

L = 6. DFB = 6. 30 in. = 180 in.

The selected extraction parachute is a stable, reasonably high-drag ringslot parachute

with long suspension lines. A ringslot parachute was used as an extraction chute for each

Apollo main parachute. Thble 5-2 in section 5.1 gives, for a ringslot parachute, a CDo of 0.56 to

0.65. A medium porosity canopy is selected with a CDo = 0.65. Using suspension lines with an

Le/D 0 ratio of 2 increases the drag coefficient by 10% (see Figure 5-20). Therefore,

CDo = 0.65. 1.1 = 0.715.

The extraction parachute to forebody diameter ratio is

Dp _ 5.0 = 2.0

DFB 2.5

and the distance behind the forebody-to-forebody ratio is

L 180 in. 6 0

DFB 30 in.

resulting in a drag loss of 13% (see Figure 5-21) and a final CDo of 0.715 • 0.87 = 0.62.

The canopy surface area, So, is

(CDSEP _26.20 ft2

So = (CS)E.62 = 42.3 ft2

CDo 0.62

resulting in a nominal parachute diameter

Do = 1.1283 VFo = 1.1283 AD3 = 7.34 ft

7-11

NWC TP 6575

A stable, 7.4-foot-diameter ringslot parachute is selected. The weight of the ringslot

extraction parachute can be estimated from section 6.7 to 2.5 pounds, and the weight of the

extraction parachute assembly including riser and deployment bag to 1.5 . 2.5 pounds = 3.75

pounds.

The weight of a single 72.7-foot-diameter main parachute, as determined from section

6.7, is 54 pounds. This weight estimate assumes an efficiently designed main canopy that has a

combination of tape and radial seams to carry the radial loads and has other, similar

weight-saving design features. The arrangement of the extraction parachute in relation to the

drone is shown in Figure 7-5.

Riser length LR = 109 In.

-• 109"1

891, -180" = 6DF8 B

FIGURE 7-5. Extraction-Parachute Assembly.

7.3.6 Pilot Parachute Assembly

The extraction parachute assembly weight of 3.75 pounds is too heavy to be deployed by

a drogue-gun slug; therefore, a small pilot chute is selected for initial deployment by the

drogue-gun slug. This pilot chute, in turn, will deploy the extraction parachute.

Evaluation of past good and poor deployments has led to the rule that the extraction force

of the pilot chute should be greater than or equal to four times the weight of the unit to be

extracted; in this case, the extraction parachute assembly. So that the pilot chute has enough

force, a pilot chute is selected that will produce, at the minimum deployment speed of 150

KEAS, an extraction force equal to five times the weight of the extraction parachute

assembly: 5. 3.75 pounds - 18.75 pounds.

The minimum dynamic pressure at 150 KEAS is

q(150 KEAS) - 25v2 150 = 76.3 lb/ft2 (see section 5.11) 2952 295

7-12

NWC TP 6575

0This results in a pilot chute drag area of

=Fp = 18.75 lb 0.25 ft2

(CDS)PC = q 76.3 lb/ft2

A fast opening, stable, box-type pilot chute, see Figure 6-32, is selected with a drag

coefficient of CDo = 0.55. The pilot chute canopy area, So, is

so = 0.25 ft = 0.456 ft2

0.55

and the parachute diameter, Do, is

Do = 1.1283Fo = 1.1283 0.456 = 0.76 ft

This is a very small parachute. A 2.0-foot-diameter box-type pilot chute with stabilizer vanes is

selected. This pilot chute has a steady extraction force, Fpc:

Fpc = (CDS)pC q

= 76 lb/ft2 1.73 ft 2 131.3 lb for 150 KEAS

= 135 lb/ft2 1.73 ft 2 = 233.6 lb for 200 KEAS

Figure 7-6 shows the pilot chute assembly in relation to the drone, and Figure 7-7 shows

the total main parachute subsystem.

-- ' 289"'

336.~..j PILOT CHUTE

L 'ýLPARACHUTE CMATEN PILOT CHUTE BRIDLE ] DROGUE GdUN SLUG

180"-6 DFB

FIGURE 7-6. Pilot Chute Asscmbly.

0

7-13

NWC ITP 6575

0- 0 -M w 0 tIT6

2C

* _PL

w IL

7-14

NWC TP 6575

7.3.7 Main Parachute Forces

7.3.7.1 Requirements

Drone weight ............................................. W D = 4800 lb

Maximum deployment speed .............................. vo = 200 KEAS

Minimum deployment speed ........................ Vo minimum = 150 KEAS

Maximum allowable total parachute force

(two main parachutes) ................................... FT = 16,000 lb

Deployment altitude .................................. H = 2000 to 7000 ft

7.3.7.2 Velocity-Altitude Profile

Section 5.5 states that the maximum opening force of the main parachute occurs at

maximum deployment altitude. Figure 7-8 shows a velocity-altitude-versus-time profile for a

typical vehicle recovery system.

The maximum dynamic pressure, qo, occurs at the 200-KEAS deployment velocity

v 2 20W2

q(200 KEAS) == -2= 135.14 lb/ft2

True velocity at maximum deployment altitude in feet per second is

vo = v7000 ft - 200" 1.69 -1- = 200.1.69.1.1455 = 386.7 ft/s

7.3.7.3 Force Calculation Methods

The opening forces of the reefed and full-open main parachutes will be determined by

three different methods described in section 5.4.6.

> 0 F R

0 a Parachute deployment 0

line stretch) 1

1 a Reefed open

2 = Disreef 2 FO

3 = Full open

FR = Reefed opening force t

FO = Full open force

TIME

FIGURE 7-8. Velocity-Time Profile.

7-15

NWC TP 6575

1. The [(C'"W method is accurate for high canopy loading W[(C-•] parachutes,

such as drogue chutes, and for the first stage of reefed parachutes. However, opening forces

calculated by this method may be only ± 20% accurate for unreefed main descent parachutes

and for the disreef stage of large main parachutes.

2. The Pflanz method is quite accurate for all conditions including high altitude, but

neglects the effect of gravity. Parachutes opened in vertical descent will have a 1-g (one weight

unit) higher force than calculated. It is necessary to calculate the canopy filling times for the

various reefed stages (see section 5.4.3) and to determine the drag-area-versus-time profile for

the specific parachute (see section 5.4.4). This method permits the investigation of variations

in filling times and drag-area-versus-time profiles.

3. The force-trajectory-time computer method includes the effects of altitude, gravity,

and changing trajectory angle. This method requires determination of a drag-area-versus-time

profile for the entire parachute opening sequence (see Figure 5-52). Computers permit

multiple runs with changes in times, drag-area-versus-time profiles, starting velocities, and

altitudes.

7.3.7.4 Reefed Opening Forces

When the [(_c)] method is used, the opening force of the reefed parachute, FR, is

FR (CDS)R . q0 . Cx. XI

where

FR = maximum allowable single parachute force FR - 16, 000 lb - 8000 lb

2

(CDS)R = reefed parachute drag area, ft2

q0 = dynamic pressure at line stretch = 135.14 lb/ft2 (see section 7.3.7.2)

C,- opening-force coefficient at infinite mass (see Table 5-2)

X - opening-force reduction factor (see Figure 5-48)

The allowable drag area of a single, reefed main parachute is

(CDS)R =FR allowable

qo" Cx7 X�7-16

NWC TP 6575

FR allowable = 8000 pounds (see section 7.3.7.1). C, for reefed opening of extended-skirt

parachutes is 1.0 to 1.1 (see Figure 5-52). XI is obtained from Figure 5-48 as a function of

canopy loading, W/(DS)R, that is calculated under the assumption that the reefed drag area

of one main parachute is about 2.5% of the fully open drag area. Therefore, the canopy loading

of the reefed parachute is

W/(CDS)R = 4800/2 = 51.28 lb/ft2

(0.025X3744)

For this canopy loading, XI is obtained from Figure 5-48 to 0.86 and

8000 lb = 62.58 ft2

(CDS)R 135.14 lb/ft2 " 1.1 0.86

This reefed drag area is less than 2% of the drag area of the full-open main parachute and may

be too small for obtaining reliable, fully reefed canopy inflation. Therefore, a 2.2% drag area

ratio is selected.

(CDS)R = 2.2% of (CDS)po = 0.022(3744 ft2) = 82.37 ft2

The opening forces for this larger reefed drag area mutt be calculated. The canopy

loading, W/(CDS), of the reefed main parachute is

W 2400 lb 29.14 Ib/ft2

(CDS)R 82.37 ft2

For this canopy loading, Figure 5-48 shows a force-reduction factor, XI, of 0.75. The

reefed opening force is now calculated

FR = (CDS)R. q0 . Cx. X, = (82.37 ft 2X135.14 lb/ft 2

Xl.1XO 75) = 9183 lb

2FR 1318,366 = 3.8g

4800

This force is higher than the allowable force of 8000 pounds per parachute (see Section 7.3.7. 1).

When the second calculation method, the Pflanz method, is used, the reefed opening

force is

FR = (CDS)R. ql. Cx. X,

X1 is a function of the ballistic coefficient, A:

2W

(CoS)p p g tf Vo

7-17

NWC TP 6575

In this equation, known values are W, (CDS), g, and vo.

The mass density of air, p, at a 7000-foot altitude is

p = f(H) = 0.0023769(0.8106) - 0.0019396 (see Table 3-3)

Canopy inflation time, tf, is calculated as follows (see [Section 5.4.3):

= = nD FCDS)R

v0 (CDS)p

tf 17(72.7), 82.37 0.49 seconds

386.7 N 3744

A 2(2400) 5.07

(82.37 ft2XO.0019396X31.28X0.49 sX386.7 ft/s)

x, f(A) for n = I/L. n = 1/z is appropriate for reefed inflation (see Figure 5-39).

X= 0.77 (see Figure 5-51)

FR (82.37 ft2X135.14 lb/ft2Xl.1X0.77) = 9428 lb

It is interesting to investigate the effects of changing the canopy filling time ± 25%. and

changing the slope of the drag area profile on the parachute opening force. For the change of

the drag area slope, a profile factor of n = 1.0 instead of n = ½ (see Figure 5-5 1) is selected.

The resultant change in opening force is shown in Table 7.1.

TABLE 7-1. Reefed Opening Force as a Function of

Filling Time and Drag-Area Profile.

If, S n = f(Cc)S) A X, FR, lb % change

0.37 0.5 4.21 0.82 9956 + 6.5

0.613 0.5 6.98 0.74 8985 -3.9

0.49 0.5 5.27 0.77 9428 0.0

0.49 1.0 5.27 0.79 9673 + 2.6

Force data obtained with the force-trajectory-time computer method are shown in the

force summary in section 7.3.7.5.

7.3.7.5 Main Parachute Disreef Opening Forces

A short reefing time, tR - to-2, helps to limit altitude losses; however, in clusters,

sufficient reefing time is required to permit all parachutes to reach full reefed inflation before

disreef.

7-18

NWC TP 6575

Tb save trajectory time, the reef-d pardchute is disreefed at a dynamic pressure 10 to 20%

higher than the terminal reefed dynamic pressure. Therefore,

q2 = 1. (C1 S)- (Figure 7-8)

q2 = 1.1 4800 lb = 4800 lb _ 4800 = 23.94 lb/ft2, and 2(82.37) + (CDS)droe 165.54 + 55 220.54

v,= - i = - 23.94(840) • 1.1455 = / ft/s (see Figure 5-112)

Parachute opening force, F0 , by the (CD"SJ) method:

Fo = (CDS)2-3" q2" Cx. XI

X1 = fI•-DS

W 2400 lb 2400 lb 0656 lb/ft2 = ~~= _ __ -- 056I/t

(CDS)2-3 (3744 - 82.4) ft2 3661.3 ft2

X, for 0.656 is 0.07 and

F0 = (3631X23.94XI.30X0.07) = 7910 lb

Opening force by the Pflariz method:

F0 = (CDS)2-3. q2' C, . XI

X= I f(A)

2W

(CDS) 2-3' P 9 tf' V2

Known variables are W. p. g, and v2.

(CDS)2-3 = (CDS)o - (CDS)R = 3741 - 82.3 = 3661.7 ft2

A 6-second reefing time, tR. ,s .2c!ected, a"d an altitude loss during the reefed stage of 500

feet is calculated (from 7CA) fe,; ic ' WOO feet). Densi:. ,, at 6500 fect is 0.0019569 slugs/ft 3.

7-19

NWC TP 6575

The disreef time, tf, is obtained by

tf = = n D. (CDS)o - (CDS)R

V2 (D)

From Table 5-6 in section 5.4.3, a canopy fill constant n = 6 is selected; therefore,

= 6(72.7). /3744 - 82.4 = 2.80(0.988) = 2.87 s

155.6 3744

A= 2(4800 ib) = 0.0471 (2X3.661 ft'XO.0019569X32.17)(2.87 sX155.6 ft/s)

From evaluation of test data, it is known that the drag-area-increase-versus-time of

extended-skirt parachutes at disreef occurs in a concave form, denoted in Figure 5-51 by the

definition n = 2. For a ballistic parameter A = 0.0471 and a drag area increase in accordance

with n = 2, the force reduction factor, X1, is 0.067, and the parachute disreef force, Fo, is

F, = (3.661 ft2X21.76 lb/ft2X1.4X0.067) = 7472 lb

Results of changing the canopy inflation time, tf, and the drag-area-versus-time profile, n, are

shown in Thble 7-2.

Reference 5-76, the Pflanz report, provides a more detailed study of the effect of canopy

fill time and drag-area-increase-versus-time profile on the magnitude of the parachute

force.

TABLE 7-2. Disreef Opcning Force as a Function of

Disreef Time and Drag-Area Profile.

th, a n = f(CaS) A X, F,,, Ib % change

2.87 2.0 0.047 0.067 7472 0

3.29 2.0 0.00402 0.0595 6648 -11.0

235 2.0 0.0563 0.074 8268 + 10.5

2.87 1.5 00487 0.080 8938 + 19.6

Force-Trajectory-Time Computer Method

The program established oy NWC determines as a function of time the parachute forces,

the vehicle deceleration, and the space-positioning (trajectory) data in a two-axis system. The

method requires a drag-area-versus-time profile for the individual parachutes and the total

vehicle system (Figure 7-9). This profile was previously shown in Figure 5-52. Figure 7-9

includes the change in air-vehicle drag caused by the change in vehicle attitude during the

parachute opening process.

7-20

NWC TP 6575

0 1 2 3 4

I I I5,198 FT 2

I5 I 5 FT2 3,713 FT

T I /IAIR VEHICLE (FT 2 952 / 2 I I SINGLE

89.6T 81.6 FT PARACHUTE

TIME. SECONDS

0 = DEPLOYMENT

1 = CANOPY/LINE STRETCH

2 = REEFED OPEN

3 = DISREEF

4 = FIRST FULL OPEN

0 TTOTAL AIR VEHICLE

(C S) (TWO MAIN PARACHUTES

D 179-30 PLUS AIR VEHICLE)

(FT I I i

0.78 1 0.49 1 2.0 1 3.51 1 3.85

TIMES I I [ - .51

(SEC) jItr -6SEC

I V 10.61 *

FIGURE 7-9. Drag-Area-Versus-Time Profile for a Single Parachute and the Total Drone.

Parachute force data calculated by the three methods are compared in Table 7-3.

7.3.7.6 Comments on Calculated Opening Forces

1. The reefed opening force for the single parachute is higher than thie

contractor-requested maximum allowable force per parachute of 8000 pounds.

7

7-21

NWC TP 6575

TABLE 7-3. Comparison of Parachute Forces Calculated

by the Three Methods.

W/(CDS) Pflanz Force-trajectory-time

method, lb method. lb computer method, lb

Reefed Opening Forces

9107

t = 0.49 s, n = 'A 9428 9255a

t = 0.61S, n = %z 8985

tj = 0.37 s, n = 1A 9956

i = 0.49 s, n = 1.0 9673

Cluster of two parachutes

tf = 0.49 s, n = / 19.133a

19,058b

h = 0.39s, n = 'A 20,132

if = 0.61 s, n = % 18,257

Disreef Opening Forces

7910

h = 2.87 s, n = 2 7472 7404

t = 3.29s. n = 2 6648

tf = 2.35 s, n = 2 8268

t, = 2.87 s, n = 1.5 8938

Cluster of parachutes

h = 2.87s, n = 2 13,120

t = 3.25 s, n = 2 12,261

t = 2.00s, n = 2 16,115

aComputer time steps At - 1100 s. bComputer time steps At = 1110 s.

2. The average disreef force is approximately 1500 pounds lower than the reefed force.

Therefore, it appears logical to lower the reefed force and increase the disreef force. Although

this adjustment probably cannot be made within the 8000-pound limit, 8500 pounds appears to

be an obtainable goal.

3. To meet the contractor requirement of an 8000-pound maximum force limit per

parachute, two-stage reefing is required.

4. It appears practical to determine in drop tests if a 2.0 to 2.1% reefed drag area can be

obtained. This drag area would decrease the reefed opening force and somewhat increase the

disreef force. However, reaching an average maximum force of less than 8000 pounds appears

doubtful.

5. In the calculations, both parachutes are assumed to have equal opening forces. In

reality, opening forces of the two parachutes can differ because of variations in filling time.

lead-ann-lag chute behavior caused by blanketing, and resultant nonuniform canopy inflation.

7-22

NWC TP 6575

The fast-opening Apollo ringsail-type main parachutes had a load distribution among

the three parachutes of 40-40-20. The individual parachutes, therefore, had to be overdesigned

in a 40/33 ratio. However, the total parachute force load taken by the vehicle hard points did

not exceed the calculated average load because of the high-low variation of the individual

parachutes.

The two slower-opening extended-skirt parachutes used for this application are more

uniform in their load distribution. A cursory analysis of available test data indicates that a

55/45 load distribution between the two parachutes and a no-overload condition for the vehicle

hard points should be an acceptable load distribution.

A contractor-subcontractor agreement is required to determine whether the individual

parachutes should be designed for the 55/45 load variation or whether this overload can be

accommodated by the 1.5 safety factor and the additional safety provided by the normal

overstrength of textile specification materials.

7.3.7.7 Snatch Forces

The snatch force is caused by the acceleration of the mass of the parachute assembly to

the velocity of the forebody (drone). A canopy, partially inflated at line stretch, increases the

mass of the parachute by the mass of the air included in the canopy; this can increase the

snatch force (mass shock) considerably.

"lTo principal rules should be followed to keep the snatch force within allowable limits.

1. Keep the parachute canopy closed until line (canopy) stretch occurs by use of a

deployment bag o! %kirt restrictor.

2. Accelerate I!: mass of the parachute assembly in incremental steps.

Known means of accomplishing these goals are discussed in Chapter 6.1.

The difference between a poor deployment and a deployment that accomplishes the first

rule and partially accomplishes ' second is illustrated in Figure 5-54, which shows snatch

and opening forces for the C-9 p. tchute with and without the quarter deployment bag. The

deployment method outlined in ! tilon 7.3.4 should hold snatch forces at a level below the

parachute opening forces.

A method for calculating ,tch forces is described in Reference 2.2, the 1963 edition of

the USAF parachute handbook. : nreferred method for calculating parachute deployment.

including the snatch force, is cont.iiiici in J. W Purvis's AIAA paper, "Improved Prediction of

Parachute Line Sail During I incs-First Deployment" (Reference 5.86).

7-23

NWC TP 6575

7.3.8 Parachute Stress Analysis

7.3.8.1 Parachute Design Data

A total parachute assembly is shown in Figure 7-10.

1. Drone bridle, two each 7. Deployment bag bridle

2. Disconnect, automatic at ground impact 8. Deployment bag IDB)

3. MP riser, two each 9. Extraction parachute riser

4. MP suspension lines, 64 per parachute 10. Extraction parachute

5. MP canopy 11. Second parachute, not shown

6. Parachute resfing system

FIGURE 7.10. Main-Parachute Asembly.

Parachute type: Conical full extended skirt

Diameter: Do = 72.7 ft

Line-length ratio: Le/Do = 1.25; Le = 1083 in.

7.3.8.2 Parachute Forces

The maximum reefed opening force, FR, is 9255 pounds. The maximum disreef opening

force, F., is 7404 pounds. The maximum design force for stressing the parachute assembly, FI,

is 9255 pounds.

The forces obtained in computer runs are selected as the most accurate forces for

stressing the parachute assembly and its components. Based on multiple computer runs, a

diligent choice must be made for the most likable forces.

7.3.8.3 Main-Parachute Safety and Design Factors

Section 6.4 is used as a guide for selecting the safety, load, loss, and design factors in

Table 7.4.

7-24

NWC TP 6575

TABLE 7-4. Determination of Design Factors for the Main Parachute Assembly (Section 6.4.2).

Assembly Safety Load factors _ _- factors Design

unit factor m 0064) 1 LF u e k r 0 LF factor

Drone bridle 1.6 ...... ... 1.6 0.8 1.0 0.95 1.0 1.0 0.76 21

MP riser 1.6 ... ... ... 1.6 0.8 1.0, 0.76 2. 1

MP suspension lines 1.5 ... 1.04 1.0 1.56 0.9 0.95 0.81 1.93

MP canopy 1.5 ... ... 1.0 1.5 0.9 0.95 0.81 1.85

Reefing system 2.0 ... .... 2.0 0.85 0.9 0.73 2.74

Pilot chute 1.5 ...... 1.5 0.85 1.0 0.81 1.85

EP riser 1.5 1.25 ....... 1.875 0.85 0.95 0.77 244

EP suspension lines 1.5 ... 1.02 1.0 1.53 0.85 0.95 0.77 1.99

EP canopy 1.5 1.. . .. 1.0 1.5 0.9 0.95 0.95 1.0 1.0 0.81 1.85

NOTE: MP = main parachute; EP = extraction parachute.

7.3.8.4 Suspension-Line Selection and Strength

The following guidelines are used for selecting the suspension lines of the main

parachutes (Thble 7-5).

TABLE 7-5. Suspension-Line Selection.

Number of suspension lines

Factors

60 64 68 72

Maximum parachute force, lb Fx 9255 9255 9255 9255

Design fh.tor (from Table 7-4) DF 1.93 1.93 1.93 1.93

Required suspension-line strenglh, lb FSL 1 297.7 279.1 262.7 248.1

Gore width, ft Eo 3.8 3.6 3.35 3.16

1. Connection of suspension lines to riser legs and drone hardpoints is made easier if the

number of suspension lines are a multiple of 4 or 8.

2. The gore at the skirt should not be wider than 3.5 feet for packing reasons.

3. The canopy should have no fewer than 12 gores to avoid gore distortion during

inflation.

4. Radial ribbons or radial seams should not overlap at the vent; overlapping causes

bunching of material and associated sewing problems.

5. The strengths of available suspension-line types may affect the gore selection.

Table 7-5 shows the required suspension line strength and the resultant gore width as

functions of the number of gore/suspension lines used.

7-25

NWC TP 6575

The width of the goie of the skirt on conical, full-extended-skirt (CFES) parachutes is

about 85% of the maximum gore width, Eo.

Sixty-four suspension lines are selected in accordance with MIL-C-7515, TIpe XI, with

300-pound tensile strength.

This selection provides a margin of safety (MS) of

MS = available strength - 1 = 300 _ 1 = 1.064-1 = 0.064

required strength 281.9

The suspension line will be attached to the canopy skirt in a loop connection.

7.3.8.5 Canopy Stress

No precise method has been d.-veloped for calculating the stress in a circular,

solid-material, bias-construction canopy.

Section 6.4 describes a semi-empirical method for determining the required fabric

strength of a solid material canopy in pounds per unit width using the stress in a pressure

vessel as an analogy. The stress in a cylindrical vessel, expressed as force per unit length, is

tc =f 2P-r(Ib/in.)

2

where p is the pressure in the cylindrical vessel and r is the vessel radius. Using this analogy

and considering the canopy gore as part of a pressure vessel, the required material strength of

the canopy per unit width is obtained

tc f D Sl

DP12

where

tý = required material strength in lb/in. width

F0 - maximum parachute force = 9255 pounds

Dp - inflated parachute diameter - DOC (see Figure 5-78)

DS - design factor, 1.85 (see Table 7.4)

-c W 9255 1.85 - 951.85 - 8.9 lb/in.

(nX72.7X0.7X12) 1918

7-26

NWC TP 6575

The maximum stress actually occurs during reefed inflation because of the smaller inflated

diameter:

Reefed inflated diameter = D Rf .(CDS)R - C = 72.7 0.02 (0.7) = 7.9 ft (CD'S)p

tc reefed inflation =-2.4 1.85 = 60.6 lb/in. 9282.4

A 1.1 ozlyd 2 material is selected in accordance with MIL-C-7020, lype I, with 42 lb/in.

breaking strength for the main part of the parachute canopy, and 2.2 oz/yd 2 material,

MIL-C-7350, Type I, with 90-lb/in. strength for the crown area that is inflated during reefed

opening.

7.3.8.6 Canopy Reinforcing Tapes

1. Skirt Tape. The skirt tape should Iv. equal or greater in strength than the individual

suspension lines but not less than 1000 pounds, and 1-inch-wide tape should be used for

parachutes larger than 20 feet in diameter.

The nylon tape selected is 1-inch-wide MIL-T-5038, Type IV, with 1000-pound strength.

Proper connection of the skirt tape to the radial seam (tape) and the suspension line must be

ensured.

2. Vent Tape. From the geometric design of the parachute vent (Figure 7-11). the force in

the vent tape, FVT, is calculated

FVT . FRT DF

NSL 2 sin[NS]

= 9255 1.85 = 1360 lb

64( 2 si)6

A 1-inch-wide, 4000-pound webbing (MIL-W-5625) or 7/8-inch-wide, 3100-pound webbing

(MIL-W-5625) is selected.

3. Vent Lines. The strength of the vent line- should be equal to or greater than 60% of the

strength of the radials.

7-27

NWC T? 6575

0

FVT

FRT

FIGURE 7-11. Vent-Tape Geometry.

7.3.8.7 Design of Radials

The following four types of radial designs are in use:

1. Radial seams with suspension lines running in channels over the canopy and attached

at the vent and the skirt as on the canopy of the C-9 personnel parachute.

2. Suspension lines running on top of the radials over the canopy and sewn at full length

to the canopy as on many heavy-duty ribtx'n parachutes.

3. Radial tapes sewn on top of or inside the radial seams, and suspension lines attached

to the radial tapes by sewing or by skirt loops (NB-7 and T-10 canopies).

4. Radial ribbons on ribbon parachutes designed to take the total radial load with

suspension lines sewn onto d e radials or connected by a skirt loop.

The following are some comments on the design of radials:

1. Making the strength of the radials 1:qtlal to 80% of the strength of the suspension lines

has been satisfactory on thousands of ribbon parachutes.

2. When tapes or suspension lines are sewn at full length to the radials, care must be

taken that fullness in the radials ensures that the radial tapes or the suspension lines are the

primary load carrying members. For an explanation of fullness, see section 6.6.4.

3. Uniform material distribution is of utmost importance when sewn tapes or lines are

used for radial reinforcemetnt.

For the radial design of the main parachute, we use a tape with 80% strength of the

suspension lint (0.8. 300 lb - 240 Ib) sewn on top of the radial scam. A 250-pound strength,

'A-inch-wide tape is selected in accordance with MIL-T-5038, 7ýpe III. Thpe and radial seams

are marked every 24 inches for proper material distribution.

7

NWC TP 6575

7.3.8.8 Check for Proper Gore Fullness

When the first parachute of a new design has been completed in the manufacturing shop,

a gore fullness check in accordance with Figure 7-12 should be conducted. A slight amount of

slack should be noticeable in the canopy fabric in both directions when all four corners of a

gore are pulled radially outward. Slack indicates that the main loads are carried by the radials

and reinforcing tapes and not by the canopy fabric. Stress folds in the canopy indicate faults in

the design or manufacture of the parachute.

PULL A-A

A PULLRADIALS

~'~EJ/u/EE~n~mI./.~md ~~SLACK

B A B PULL .

PULL

SKIRT TAPE I VENT TAPE 8_8

FIGURE 7-12. Tlnch Check on Gorc Fullness.

7.3.9 Canopy Gore Shape

A full-extended-skirt parachute is selected that has a conical top with a 25-degree cone

angle; a nominal diameter, Do, of 72.7 feet; and 64 gores.

Based on the definitions in Figure 7-13. the canopy gore dimensions are

Base gore angle -y = 360 deg = 360 = 5.625 deg

NSL 64

Cone angle A = 25 deg

Gore Angle =sin t [Cos A ~in - sj]1

13 = sin-'IO.9063(sin 2.8125 deg)]

13 sin-'(O.9063X).0491) = 2 sin-' = 0.04447

13 = 5.1 deg

7-29

NWC TP 6575

Canopy surface area So = 4160 ft2 (see section 7.3.3)

Gore height h, = (0.653 S,)(144) cot -y12)

NSL" oS plL

h = (0.653X4160X144X20.34)

V(64X0.9063)

h= = 370.3 in.

h2 - 0.286h l = 0.286(372.73) = 105.9 in.

el = 2h, (tan 03/2) = (2X372.73X0.0445) = 32.96 in.

e2 = 0.857el = 0.857(33.88) = 28.24 in.

hs = hl + h2 - 370.3 + 105.9 - 476.2 in.

, e,

FIGURE 7-13. Gore Layout for Gore Dimensions.

7.3.9.1 Vent Area

A vent area, SV, is selected that is equal to 0.25% of the total canopy surface area, SO;

therefore,

Sv - (0.0025)So - 0.0025(4160) = 10.4 ft2 and the

vent diameter, Dv - 1.1284 SFS-v 1.1284 4 -104 3.64 ft

7-30

NWC TP 6575

0 This is a large vent opening for a reefed parachute. Several criteria may be used to determine

the size of the canopy vent as follows:

1. Unreefed parachutes with vents up to 1% of the canopy surface area, So, have been

operated successfully.

2. Reefed parachutes require a vent diameter, DV, smaller than the reefing line circle,

diameter DR, of the parachute; Dv is smaller than DR (see section 5.6, Figure 5-66).

3. The radials at the vent should not overlap. A 1-inch free space between radials is

desirable (see Figure 7-14).

NO OVERLAPPING

FIGURE 7-14. Vent Construction.

7.3.9.2 Vent Diameter

A vent construction is selected with a 1-inch free space between 1-inch-wide radials; this

results in a vent circumference of 64 + 63 = 127 in. and a vent diameter of

127

DV = L- 7 =40.43 in.

A 3-foot vent diameter is selected. The radius is 18 inches, and vent height, hy, is calculated

hv - r(cos y/2); gore half angle y/2 = 2.55 deg

hV - 18(0.999) = 17.98 in.

Manufactured gore height, h., is

hg = hl - hv - 370.3 - 17.98 = 352.32 in.

Vent gore width, ev,

ev = 2hy tan p/2 = 2(17.98X0.0445) = 1.6 in.

7

7-31

NWC TP 6575

Stress in the canopy gore area can be relieved by making the gore at the vent 10% wider

than the calculated gore dimension, ev. Therefore, ev* - 1.1 . ev - 1.1(1.6) = 1.76 inches. The

vent tape is sewn to the vent at the original ev dimension, thereby gathering the vent 10% and

creating a stress-relieving arcing in the gore fabric next to the vent. See Figure 7-15 for an

example of final gore dimensions.

h. = 476.2 in.

h, = 370.3 in.

h2 = 10O.9 in. h,

hv - 17.98 in.

ei = 3296 in. i.

=2 - 28.24 in.

ev = 1.6 in.

ev' = 1.76 in.

FIGURE 7415. Final Gore

Dimensions.

7.3.10 Pocket Bands

The pocket bands used on every gore make canopy inflation more uniform and

eliminates long and short filling times. A narrow tape is used as the pocket band, which will :ot

affect the average length of the canopy filling time. Data on the dimensioning of pocket bands

are given in section 6.4. As shown in Figure 7-16, the pocket band dimensions are

es = e2 - 28.24 in. (See Figure 7-15.)

Lb 0 0.14eS = 0.14 - 28.24 - 3.95 in.

L&- 0.238es - 0.238- 28.24 = 6.7 in.

A 5/8-inch-wide tape, MIL-T-8363, "ype I, is selected as pocket band material.

Important Note: Pocket band length, L, must be long enough to ptrinit the full

inflation of the parachute canopy.

7-32

NWC TP 6575

lLa

b�FIGURE 7-16. Pocket Band Arrangement.

7.3.11 Parachute Reefing

7.3.11.1 Length of Parachute Reefing Line

The drag area of a single reefed main parachute was calculated as (CDS)R = 82.37 square

feet (see section 7.3.7.4). This area results in the following reefing ratio:

(CDS)R _ 82.37 = 0.022 = 2.2% of So

(CDS)o 3744

Reefing by the skirt-reefing method is selected (see section 5.6, Figure 5-66 and section 6.5).

From Figure 5-72, we obtain for an extended-skirt parachute with a reefing ratio c = 0.22,

a reefing-line ratio:

T= DR/Do = 0.07

and the diameter of the reefing-line circle, DR:

DR = (0.07)Do - 0.07. 72.7 ft = 5.09 ft

and the installed length of the reefing line, LRI:

LRL = DR '7r = 5.09 IT = 15.99 ft = 191.88 in.

7-33

NWC TP 6575

The diameter of the reefing line circle, DR, is larger than the 3.64-foot vent diameter of

the canopy, Dv. This difference in diameters is an important design requirement (see section

7

.3.9).

7.3.11.2 Strength of the Reefing Line

The force in the reefing line is determined according to information in section 5.6.8. Test

items 22 and 23 in Figure 5-76 closely resemble the main parachute used here. A reefing-line�force-to-reefed-parachute-force ratio of 2.5% is selected for this assembly. Therefore, the

force in the reefing line is

(0.025)FR = 0.025(9255 Ib) = 231.4 lb

The design factor, DF, for the reefing system was determined in section 7.3.8, Table 7-4, to

be 2.74.

Required reefing-line strength, FRL.,=..., is

FRL,,.,. = DF. FRL = 2.74 . 231.4 lb = 634 lb

A coreless braided nylon line, MIL-C-7565, Type III, with a tensile strength of 750

pounds, is selected as reefing line.

Section 6.5 discusses reefing system design and installation details.

7.4 HIGH-SPEED DROGUE CHUTE ASSEMBLY

7.4.1 Requirements

The following operational requirements govern the design of the first-stage drogue chute:

1. The drone must be recoverable from any conceivable flight condition during the

engineering test phase.

2. An out-of-control drone or a drone that loses radio contact with the controller must be

prevented from flying off the range. Recovery is initiated by an independent range signal. This

type of recovery requires a high-speed deceleration parachute that can be deployed and

operated when the drone is moving at maximum speed, or is in a spin, or during any other

abnormal flight condition.

This type of recovery established the following requirements for the type and size of the

drogue chute:

7-34

NWC TP 6575

1. The drogue chute must have reliable operation in the velocity range from 200 knots at

sea level to Mach 1.5 at 50,000 feet.

2. Stability must be better than :: 3 degrees.

3. Minimum weight and volume is mandatory.

4. The drogue chute must be able to decelerate the drone to the permissible opening

speed of the main parachute assemblies.

5. The drogue chute must be suitable for the operational environment.

Figure 7-17 shows the altitude-velocity flight envelope of the drone.

\

7.4.2 Drogue Chute Selection

Thbles 5-1 through 5-5 in Chapter 5 list commonly used parachute types. Table 7-6

evaluates possible drogue chute candidates. Of the parachute candidates, only the conical

ribbon and the hemisflo ribbon have been used successfully for similar applications.

A 25-degree conical ribbon parachute is selected for this application. The conical ribbon

parachute meets all requirements and has a higher subsonic drag coefficient than the equally

7-35

NWC TP 6575

TABLE 7.6. Drogue Chute Candidates.

Type Stability Supersonic Drag coefficient Supersonic

experience Subsonic Supersonic load factor

Guide surface 0 to *2 Limited 0.3 to 0.4 0.2 to 0.34 1.7 to 2.0

Annual < *6 None 0.85 to 0.95 Unknown Unknown

Cross 0 to *3 Limited 0.6 to 0.85 Unknown Unknown

Ribbon, conical 0 to *3 Extensive 0.55 0.4 to 0.55a 1.

5b; (1.2)

Ribbon, hemisflo 0 to 2 Extensive 0.45 0.3 to 0.45a 1.25; (1.15)

Ringslot 0 to :5 None 0.65 Unknown Unknown

Rotafoil 0 to • None 0.85 to 0.99 Unknown Unknown

a See section 5-8.

b See Figure 5-50.

suited hemisflo parachute. The subsonic drag coefficient determined the parachute size and

its associated weight and volume. Numerous conical ribbon parachutes have been used

successfully at this speed and diameter range.

Based on section 5.8, Figure 5-93, we obtain the following drag coefficients versus Mach

number data:

Mach number 1.5 1.3 1.1 1.0 0.8

CDo 0.42 0.5 0.52 0.55 0.55

These CDo coefficients do not take into account a loss caused by forebody wake.

7.4.3 Required Drogue Chute Diameter

The size of the fully open drogue chute is determined by the requirement that it must

decelerate the 7200-pound drone to the allowable opening speed of the main parachute, which

is governed by the requirement that the opening force of the two main parachutes must stay

within the 9350-pound-per-chute limit established for the 200-knot opening speed of the

4800-pound drone.

A preliminary calculation shows that a terminal velocity of about 175 KEAS is required

to limit the opening load of the reefed main parachutes to 9350 pounds. A 13- to 14-foot�diameter drogue chute is needed to meet this requirement.

To reach 175 KEAS at main parachute line stretch, the drogue chute will be disconnected

by an aneroid sensor at about 7000 feet mean sea level (MSL) while descending vertically from

high altitude. The drone will free-fall for 0.8 second until main parachute line stretch occurs;

the free-fall causes a 10-knot increase in velocity. In addition, the changing density, p, results in

7-36

NWC TP 6575

about 5 KEAS Av compared to equilibrium velocity. We therefore design for a terminal

velocity of 175 - (10 + 5) knots, or 160 KEAS.

Dynamic pressure, q, at 160 KEAS = 16-0 = 86.78 lb/ft2

295

Required drogue chute drag area, (CDS)p = 7 lbt2 2 82.95 lb/ft2

q 86.8 ib/ft =

Drogue chute canopy area, So = (CDS)p = = 150.9 ft2

CDo 0.55

Nominal diameter, Do - 1.128off = 1.1284509 = 13.85 ft and the inflated

diameter Dp = DO C = 13.85 0.65 = 9 ft.

The drag coefficient will be reduced because of the forebody wake and will increase if

suspension lines are longer than Le/Do = 1.0.

Figure 7-18 shows the arrangement of the drogue chute.

__Dp 9 FT

DFB-2, 5 FT 29~OF

L,/Doz 1.6 (13.8S 12) =2491n.

Dp/DFO = 0/2.5 - 3.6

FIGURE 7-18. Drogue Chute Arrangement.

Suspension lines equal in length to 1.5 Do, are selected, causing an 8.5% CDo gain,

(see Figure 5-20). The loss in drag caused by forebody wake is determined from Figure 5-21.

The ratio of inflated parachute diameter, Dp, to forebody diameter, Dpj, is 3.6, and the ratio of

the distance between the leading edge of the inflated parachute and the aft end of the drone is

300/30 in. = 10 as shown in Figure 7-18.

7-37

NWC TP 6575

The gain in drag caused by the longer suspension lines and the 5% loss in drag caused by

forebody wake (Figure 5-21) result in a final drag coefficient, CDo, for the drogue chute of

CDo = 0.55. 1.085 . 0.95 = 0.57

and a corrected drogue chute diameter

Do - 13.61 ft

7.4.4 Computer Analysis of Drogue Chute Performance

At this point, a computer program should be established to determine the following

performance conditions:

1. Balance reefed and disreef parachute forces and filling times. Start at Mach 1.5 at

34,000 feet (see point () on Figure 7-17). Check final selection for a 10,000-foot-altitude

condition.

2. Determine required opening altitude for high-speed, low-altitude deployment. This

requires trajectory runs with both the drogue and main parachutes.

3. Determine maximum horizontal range, including prevailing wind conditions.

4. Verify that the selected main parachute opening speed of 175 KEAS is reached for all

important flight conditions and that, for an opening velocity of 175 KEAS, the main parachute

forces stay within the allowable force limit of 9255 pounds.

5. Include opening of the air bags with a 6.0-second inflation time in some of the

trajectories. Inflation starts after main parachute opening.

The prime contractor should point out any special flight conditions that may require

parachute recovery. The prime contractor will probably also perform recovery computer runs

to determine for which flight conditions and from what altitudes recovery can be

accomplished.

7.4.5 Flight Emergency Recovery Conditions

Certain flight conditions other than recovery command from the flight controller or the

range safety officer may result in automatic on-board recovery command. These conditions

include

1. Loss of RF link.

2. Loss of engine power (glide on internal power).

3. High accelerations in x, y, and z caused by out-of-control flight conditions or in-flight�afflicted damage on target drones.

7-38

NWC TP 6575

7.4.6 Drogue Chute Opening Forces

Parachute opening forces should be obtained from the computer program. However, a

hand calculation is required for defining the force range before setting up the computer

program. Furthermore, canopy filling times and force coefficient, C,. must be determined

before computer runs (see section 5.4).

Determining the drogue chute opening forces with the W/CDS method is normally

sufficiently accurate for high-canopy-loading drogue chutes. If no computer backup is

available, the Pflanz method (see section 5.4.6) will provide good force data.

7.4.6.1 Drogue Chute Reefed Opening Forces

When the W/CDS method is used, the reefed opening force, FR, is calculated to

FR = (CDS)R. q. C,. X

and the maximum allowable drogue chute drag area with a 2Z000 force limit is calculated to

(CDS)R FR

q'-Cx'-X,

i where

FR, the maximum allowable force, is 22,000 lb

q, the maximum dynamic pressure, is 813.9 lb/ft2

For supersonic application, Figure 5-50 in section 5.4 shows CK = C' . X1 for the

supersonic deployment of conical ribbon parachutes. Most applicable are the data for the

Mercury and the Cook conical ribbon parachutes, which were deployed at velocities up to

Mach 1.6. CK factors of 1.3 to 1.75 have been measured in supersonic deployment of conical

ribbon parachutes. Forebody wake and poor deployment greatly affect the force coefficient.

Mortar deployment often produces bag strip-off before canopy stretch, causing premature

partial canopy inflation and a high X1 factor. Rocket extraction or drogue gun/pilot chute

deployment, both resulting in canopy stretch before skirt inflation, generally avoid this

problem. A force coefficient C, = 1.25 is selected.

X, is a function of ( that is unknown at this time, but (based on experience) is

(CDS)R

estimated to be 0.95 and corrected afterward:

22,000 lb (CDS)R = (813.9 lb/ft2X1.25X0.95) = 22.76 ft 2

7-39

NWC TP 6575

The canopy loading of the reefed drogue chute is

WdM 7 7200 7200 = -d, ! - -- 316.3 lb/ft2

(CDS)R 22.76 22.76

for this )'. Figure 5-48 shows X1 = 1.0; the corrected reefed-drogue-chute drag area is

calculated

(CDS)R - 22,000 lb

(813.9 lb/ft2

Xl.25X1.0) = 21.62 ft2

The required reefing-line length for obtaining this drag area can be determined from

Figure 5-73, section 5.6.6, using the method of section 7.3.11.

7.4.6.2 Drogue Chute Disreef Opening Force

An important factor to determine is reefing time. A long time is required to reach close to

terminal velocity before disreef. A practical approach, based on experience, is to select the

1.1-times-terminal-velocity point for disreef. If this time is too long, then a shorter reefing time

is required, resulting in a higher disreef velocity and forces.

The terminal velocity of the reefed parachute is

Wd =x 7200 lb 7200 qterminal (CDS)R + (CDS)drone I 21.62 + 0.115 .75 ft2 '_ 30.26

qterminal - 237.9 lb/ft2 = 265 KEAS

Disreef occurs at 1.1 (qterminal) = 1.1(237.9) - 261.7 lb/ft2.

The disreef force is

Fo - (CDS)-q. q. Cx. X,

C, for disreef is 1.10

X1 - f

W 720 86.8 lb/ft2 and X1 from Figure 5-48 -0.92

(CDS)D 82.95

7-40

NWC TP 6575

and disreef force, Fo, is calculated

Fo - (CDS)D. q. C. X!

Fo - (82.95X261.7)(1.10XO.92) = 21,%8 lb

Both forces FR and Fo are close to the allowable force limit of 22,000 pounds. Because

loads vary 5 to 10%, slight overloads may occur. However, the 7200-pound drone weight is the

take-off weight. Off-range recovery and conceivable emergencies will occur at lighter drone

weights, resulting in lower parachute forces.

7.4.7 Drogue Chute Stress Analysis and Design

Dimensioning of the various components of the parachute assembly involves three

primary tasks (1) establishing design and safety factors, (2) determining the loads and stresses

in the assembly components, and (3) dimensioning all assembly members. The methods used

for these tasks are described in section 6.4.

7.4.7.1 Drogue Chute Safety, Load, Loss, and Design Factors

The method used is similar to the one developed in section 6.4. Table 7-7 shows safety,

load, and loss factors in relation to design factor.

TABLE 7-7. Determination of Design Factors for the Drogue Chute.

7.4.7.2 Number of Gores and Suspension-Line Strength

The drogue chute will be designed for a maximumn force, Fo, of 22,000 pounds in the

reefed and full-open stages. The suspension-line arrangement was selected in accordance with

Table 7-8.

TABLE 7-8. Effect of Number of r- "pension lines/Gores on Required

Suspension-line Strength, Gore Width, and Vent Diameter.

Number of suspension lines

Factors 16 20 24 28

Design factor, Dr, from ifble 7.7 2.78 2.78 2.78 2.78

Required suspension-line strength, lb" 3823 3058 2548 2184

Approxdmate gore width, ft 2.7 2.18 1.81 1.55

Minimum vent diameter, D,, fib 0.85 1.06 1.27 1.48

Area ratio (SJS..,) - 100% 0.376 0.585 0.839 1.14

Suitable suspension line, MIL-C-7515 type IX IX Vill VII

Specification strength, lb 4M00 4000 3000 2500

1 The suspension-line strength is determined by FSL = F./NSL.

b The minimum vent diameter is determined by the requirement that radials

do not overlap at the vent.

A canopy with 24 gores and 3000-pound-individual-strength suspension lines is selected

primarily for gore width and vent diameter. The relatively large vent must be covered with wide

vent lines held in place by proper connections.

The method described in section 6.4 is used for preliminary dimensioning of the

horizontal ribbons. In this method, the expression Fo/(CDS)p is an indication of the pressure in

the parachute canopy; the gore width, es, is an indication of the gore radius. A smaller gore

width and resultant gore radius causes lower stress in the individual horizontal ribbons for a

given internal pressure. Figure 6-41 shows boundary curves for the required horizontal ribbon

strength. These data, based on analysis of many tested ribbon parachutes, were first presented

in Reference 5.39 and subsequently updated by the author.

For the reefed parachute,

FR/(CDS)R = lb _ 1017.6 Ib/ft2

21.62 ft 2

The gore width of the reefed parachute is obtained from the following consideration. The

reefed drag area is equivalent to the drag area of a parachute with the following nominal

diameter (DRJ):

SS ,d= (CDS)R = 21.62 ft2 = 39.31 ft2

CDo 0.55

The equivalent nominal diameter for the reefed parachute is

DRo = 1.128IJo = 1.128/39.31 = 7.07 ft

7-42

NWC TP 6575

and the gore width is

ers MDRo (7.07)n - 0.93 ft NSL 24

For an of 1017.6 lb/ft2 and gore width of 0.935, Figure 6-41 requires a horizontal (CDS)p

ribbon strength of 500 pounds. For the fully open parachute, we obtain Fo to (CDS)p

22,000 lb . 265.2 lb/ft2 and es to 1.8 feet. This condition requires a horizontal ribbon with

82.95 ft2

200-pound strength.

"TWo-inch-wide ribbon with 460-pound strength, MIL-T-5608, Trype DII, is selected for the

upper canopy part, and 2-inch-wide ribbon with 300-pound strength, MIL-T-5608, Type CV, is

used for the lower part of the canopy. This drogue parachute will be subjected to

high-frequency ribbon flutter during its high-speed descent from altitude, which may include a

descent on the drogue chute from 50,000 to 7000 feet. Disintegration of horizontal and vertical

ribbon and the stitching connecting the ribbons has occurred in the past during long-duration,

high-speed applications of reefed and unreefed ribbon chutes. This high-frequency flutter is

especially pronounced on the uninflated part of reefed ribbon parachutes.

Experience has shown that the following design features will counteract this problem:

1. Tight spacing of vertical ribbons.

2. wo vertical ribbons, one on each side of horizontal ribbon.

3. Three rows of stitching with F-F thread in the vertical ribbon.

All three features are used in this canopy design.

7.4.7.3 Design of Radials, Vent and Skirt Tape, and Vent Lines

Radials. Based on experience, radials are designed to have 80% of the strength of the

suspension lines; 0.8 3000 = 2400 pounds. Three 2-inch-wide tapes of MIL-T-5608 form each

radial; two 1000-pound Class Eli tapes and one 460-pound Class DII tape give each radial a

combined strength of 2460 pounds. It may be possible to use only two 1000-pound strength

tapes that have 80% of the actual load of 2548 pounds.

Skirt and Vent Tape. In accordance with the discussion in section 7.6.6, the selected skirt

tape is equal in strength to the suspension line but is 2 inches wide. Nylon tape (MIL-T-5608,

Class E, lype V) with 3000-pound strength meets this requirement.

The required strength of the vent tape is

Fvz = FRT DF . (2548X0.8X2.68) - 5463 10,554 lb

2 sin360 2 sin 15 deg 0.5176

NSL

Because some of this load will be taken by the vent lines, a double 4000-pound webbing is

chosen in accordance with MIL-W-2756, lype IL.

Special attention is required to obtain a design that achieves proper connection between

radial tape, vent tape, and vent lines.

Vent Unes. The vent lines should have 60% of the strength of the radial tapes and be 5%

shorter than the finished vent diameter.

7.4.7.4 Drogue Chute Riser Design

The drogue chute riser is formed of bundled suspension lines. This design eliminates the

20% connection loss, u, on the parachute side and permits a highly efficient connection on the

drone side. The individual lines must be secured against each other to prevent flutter abrasion.

Each line runs from a loop on the canopy radial, down the riser, around the drone connection

point, and up the riser to an opposite radial-tape loop. Tests should be made to determine the

strength of the radial-tape and suspension-line-loop connection and the individual loop

around the drone hard point. A wrap-around keeper is used on the riser suspension line

transfer point.

7.4.8 Aerodynamic Design of Ribbon Parachute Canopies

The two most important aerodynamic features that determine the design of a ribbon

canopy are (1) canopy porosity, XT; and (2) vertical ribbon spacing, a, which influences

effective porosity, Xk.

7.4.8.1 Canopy Porosity

The porosity of a ribbon canopy is defined as the percentage ratio of openings in the

canopy plus the material porosity divided by the total canopy surface area. Canopy porosity

affects parachute stability, drag, and opening process. A canopy with high porosity provides

for good parachute stability, and uniform, low force inflation, but also lower drag than a

canopy with lower porosity. Too high a canopy porosity may result in no or only partial canopy

inflation.

The operational porosity limit decreases with decreasing parachute diameter from about

35% total porosity for a stable 3-foot-diameter parachute to about 12% porosity for a

100-foot-diameter parachute (see Figure 6-23 (a) and Table 6-3). Section 6.2.4 discusses the

effect of canopy porosity on the design and performance of ribbon parachutes.

Properly designed conical ribbon parachutes with the correct porosity have an oscillation

equal to or less than 2 to 3 degrees; a drag coefficient, CDo, of 0.55; and an opening-force

coefficient, C., of 1.05 to 1.07 for subsonic applications with low forebody drag, such as

experienced in wind-tunnel tests.

The vertical ribbon spacing discussed in section 7.4.8.2 is of utmost importance for

supersonic application. A canopy porosity of 25 to 26% in accordance with Figure 6-23,

Curve III, and Thble 6-3 is recommended for this application.

7.4.8.2 Vertical Ribbon Spacing

Ribbon parachutes in the past were designed with individual gores, and the gores were

connected with radial ribbons and several rows of stitching. This arrangement created the

"venetian blind effect" shown in Figure 7-19. The venetian blind effect increases the effective

canopy porosity discussed in section 6.2.4.

More recently, ribbon canopies have been designed with continuous horizontal ribbons,

a design that offers savings in weight and cost. This design is described in detail in section

7.4.10.

Figure 7-20 shows the basic arrangement of a canopy gore and ribbon grid consisting of

horizontal and vertical ribbons.

/f

,/

/

FIGURE 7-19. Venetian-Blind Effect of

Horizontal Ribbon in a Ribbon Canopy.

7-45

NWC TP 6575

ev

// /1 ",hh,

hs60h

6~ / b

Nominal diameter, D.

Cone angle,. g Number of gores, No

Gore angle, 0

Gore area, S.

Vent area, Sv

Number of horizontal ribbons. NHR Number of vertical ribbons. NVRb

Gore height, hs r Gore width, es VERTICAL RIBBON B

Unfinished Finished widthat width at vent. vent, a,, e: HORIZONTAL RIBBON%,, ! i• _

Horizontal ribbon spacing, b

Vertical ribbon spacing, a Vertical ribbon width, A Aa

Horizontal ribbon width, B

Ribbon grid height. hg RIBBON GRID

FIGURE 7-20. Canopy Gore Layout.

Section 6.2.4 explains the relationship of canopy loading, W/(CDS)p; effective porosity,

Ne; and vertical ribbon spacing, a. Ribbon parachutes used as final descent parachutes use a

vertical ribbon spacing to horizontal ribbon width a/B of 2.5 to 4.0. This spacing allows

advantage to be taken of the change in effective porosity. High-canopy-loading ribbon

parachutes, such as first-stage drogue chutes, use a vertical ribbon spacingof I to 2 to avoid the

negative effects of the change in effective porosity. A narrow vertical ribbon spacing of 1.25

times the width of the horizontal ribbon width will be used for the drogue chute.

7

7-46

NWC TP 6575

7.4.8.3 Drogue Chute Summary

Parachute type 30-deg conical ribbon

Parachute diameter Do 13.61 feet

Suspension-line ratio 4/Do 1.5

Canopy porosity XT 25 to 26%

Vertical to horizontal ribbon spacing a/B 1.25

7.4.9 Canopy Gore Design and Porosity Check

7.4.9.1 Canopy Gore Calculation

Preliminary nominal parachute Do - 13.61 ft (Section 7.4.3)

Number of gores NG = 24

Canopy cone angle X - 30 deg

Canopy surface area So = 145.48 ft2

Vent area Sv < 0.01 So

Labeled with the definitions from Figure 7-20, the individual gore dimensions are as follows:

Gore area, Sg - - 145.48 ft2 . 6.06 ft2 - 872.9 in2

NG 24

Gore half angle, 03/2:

sin 13/2 - cos isin

sin 0/2 -cos 30 deg[in -3]- - 0.8660.1305) -0.113

03/2 - 6°29' - 6.48 deg

gore angle 13 - 12.96 deg

cos 13/2 - 0.99361

tan 13/2 - 0.11368

7-47

NWC TP 6575

Gore radius, rs: 1

.9.. [,r '

rs- in Pl-cos p/2)j 0.13(o.9936)

rS - 88.44 in.

Gore height, hs = rs (cos 13/2) - (88.44 in.XO.99361) = 87.87 in.

Gore width, es = 2rs(sin 13/2) (2X88.44X0.1137) - 20.11 in.

Vent area criteria:

1. Sv <0.01 So

Sv < 0.01(145.48 ft2) - 1.45 ft2

2. Dvir • 24 width of radial ribbon with no between spacing at vent

'ir. Dv > 24(2.0) - 48 in

Dv- 48 15.28 in. - 1.27 ft 0

SV - (15.28A0.7854) , 183.37 in2 _ 1.273 ft2

Sv 1.273 0.00875

ST 145.48

Therefore, S' is less than 1%.

so

Vent height, hv:

hv - rv cos - T cos

hv - 7.64(0.9936) - 7.59 in.

Ribbon grid height, hg - 87.87 - 7.59 - 80.28 in.

0

7-48

NWC TP 6575

All previous gore dimensions and the dimensions shown in Figure 7-21 are preliminary.

The horizontal ribbon spacing, b, is controlled by the required porosity, k. Required changes

in horizontal ribbon spacing may result in slight changez in gore and canopy dimensions.

7.74"

88.44" 87.87"

80.28'

ý -- 20.11 •L •

FIGURE 7-21. Preliminary Gore Dimensions.

7.4.9.2 Preliminary Gore-Porosity Check

TWo methods of calculating gore porosity are in use. The older method, described in

Reference 5.39, has been updated in this chapter. This method allows calculation of the

porosity for preliminary design purposes when no final gore drawings are available.

Reference 2.2 shows how to calculate canopy porosity if a drawing is available based on the

ratio of open spaces to total canopy area. Both methods include an estimation of the ribbon

(material) porosity.

7.49

NWC TP 6575

The total canopy porosity, XT = Xg + km where

X - gore porosity, %

-m canopy fabric porosity, %

Figure 7-20 shows that the porosity of a perfect ribbon grid, Xs., can be calculated '3:

X98 - porosity of slot area = ab

total grid area (a + AXb + B)

From the evaluation of numerous porosity calculations, the following estimate can be

made:

\T= KX- A

where

A = 2 to 3%

The porosity of a ribbon grid with variations in the distance of the horizontal ribbons is

now calculated. The total porosity is estimated, and the most likable horizontal ribbon

distance is selected for the first gore-porosity check (Thble 7-9). The widths of the vertical

ribbon, A, and the horizontal ribbon, B, are fixed values. The ratio of vertical ribbon spacing,

to horizontal ribbon width, a/B, was previously selected to 1.25, which is equal to 2.5 inches. A

horizontal ribbon distance, b, of 1.1 inches is selected as first approach based on data in

Thble 7-9.

TABLE 7-9. Grid Porosity as Function of Horizontal Ribbon Distance, b.

Desired total porosity, XT % 25 to 26% (see section 7.10.8.2)

Selected horizontal ribbon spacing, b inches 1.0 1.05 1.1 1.15

Calculated grid porosity, Xg1 % 26.67 27.54 28.39 29.21

&X -g,.25.5% (XT) % 1.17 204 289 3.71

7.4.9.3 Recheck of Gore Dimensions with Vertical Ribbon Spacing,

b, Equal to 1.1 Inches

With b equal to 1.1 inches, a gore recheck is required to determine the resultant number

of horizontal ribbons and the gore height. The number of horizontal ribbons, NHR, that can be

spaced in the gore grid height, ti, is

NHR - h,-B 80.28-2.0 . 25.25 (see Figure 7-20) (B + b) (2.0 + 1.1)

7-50

NWC TP 6575

'lb avoid a decrease in parachute diameter, 26 horizontal ribbons are selected, changing the

gore dimensions from those shown in Figure 7-21 to those shown in Figure 7-22.

Final Parachute Dimensions: 7.59"

Diameter. D, 14.07 ft

Canopy surface area, S, 15S.5 ft2

Gore area. S. 6.48 ft 2

Vent area, S" 1.23 ft2

rs-90.77"

rg=8 3 .l 3 " 82.6"

90.19"

FIGURE 7.22. Final Gore Dimensions.

hs=26(2.0 + 1.1) +2.0 = I(26X3.1)J +2 = 80.6 + 2.0

hg= 82.6 in.

es = 20.11 826 - 20.69 in,

80.625

hs=hg + hv 82.6 + 7.59 = 90.19

eshs -20.69(90.19)

= _ .2i2= 64 t

S 1= *-j- 2-93 . 2i 2 = 64 ft

7.51

i I

I8

NWC TP 6575

So 24 S9 24(6.48 ft2) - 155.5 ft2

Do 1.1284 f/ - 1.1284/rf55 -5 14.07 ft

1

Gore radius, rs - hs I

cos P/2

rs - 90.19 1 - 90.77 in. 0.99361

Radius of ribbon grid height, rg - hg - 83.13 in. The number of

cos #/2 0.99361

vertical ribbons, NVR, is five, based on free spacing of 2.5 inches and horizontal ribbon

spacing, b, of 1.1 inches.

This change in diameter from 13.67 to 14.07 feet increases the parachute drag area by 6%,

decreases the final rate of descent by about 3%, leaves the reefed opening foce unchanged,

and slightly increases the disreef opening force.

7.4.9.4 Gore-Porosity Recheck

Geometric gore porosity, Xk-- Xa + [s [ 100 - J --SRRX"

Grid porosity, Xg = 28.39% (See Table 7-9.)

Open vent area, Sv = 1.272 - 0.59* _ 0.683 ft2

Canopy area, So - 155.50 ft2

Area of radial ribbons, SRR = (rgXBXNsL) = (83.7 in.X2.0 in.X24) = 4017.62 in.

27.90 ft2

S2 F 0.683 100 - 28.3911 =F27.9023

S- 28.39+ [155.50 [ 100 .50 28.3L5

- 28.39 + [(0.0044X0.7161)] - [(0.179X28.39)J

- 28.39 + 0.0032-5.08 - 23.31%

Area covered by vent bands.

7-52

NWC TP 6575

Material porosity,

F• F[ Xs1.0 . - SRR+SVR+

Ribbon Specification Porosity, )Xm*:

The upper half of the gore uses 500-pound ribbon; X = 0. The lower half, encompassing

75% of the gore area, uses 300-pound ribbon; X. = 150 ft3/ft 2/min.

The conversion from material porosity to geometric porosity at 1/2-inch H20 pressure is

27.4 ft3

/ft 2 min = 1% k. Therefore,

= 150(0.75) = 4.1%

27.4

SV = 0.683 ft2

SRR = 27.90 ft2

Area of vertical ribbon covering horizontal ribbon, SVR:

SVR= NG-• A [hg - [(NHR - 1]]= (24)(5)(0.625)[82.6((27. 1)1.1)]

= 38.7[82.60- ((26X1.1))] = (38.7)(54.0) = 2089.80 in2

= 14.51 ft2

Area of skirt band, SSB:

SSB - Nges - (24X20.69 in.) = 4%.56 in2 = 3.45 ft2

km = (15OX0.75) 1.- (23.31 + 0.683 +27.90 + 14.51 + 3.45 f 27.4 1 100 155.50 J

= 4.106 1.0 - 0.2331 + 46543 4.106[l.0 - 0.5324]

= (4.106X0.4676) = 1.92%

Tbtal canopy porosity, XT = Xg + Xm = 23.31 + 1.92 = 25.23%. This porosity falls into the

specified range of 25 to 26% as established in Table 7-6. Porosity should be cross-checked with

the method outlined in Reference 2.2.

7-53

NWC TP 6575

7.4.9.5 General Comments on Gore Design and Porosity Selection

The canopy gore design-total canopy porosity, XT; spacing of vertical ribbon; size of

vent; and pocket-band arrangement-are the primary design features that determine the

aerodynamic performance of the parachute. The most important characteristics of parachute

performance are stability, smooth opening, drag, and opening-force coefficients.

Determining porosity under a no-load condition is rather unrealistic, because most of the

important aerodynamic characteristics occur under high-load conditions (opening shock) or

medium-load conditions (descent). However, since the beginning of parachute development,

aerodynamic parachute characteristics obtained in wind-tunnel and free-flight tests have been

related to fixed design dimensions such as diameter and porosity.

Determining the effective porosity caused by the changing load during the opening

process and by the venetian-blind effect of the ribbon grid design is practically impossible.

Furthermore, the change in effective porosity is similar on all ribbon parachutes because of the

similarities of the ribbon grid designs, load factors, and related changes in material elongation

that cause deformation of the ribbon grids and the parachute canopies.

7.4.9.6 Computer Programs for Determining Gore Design and Porosity Calculation

Both gore design and porosity calculations can be determined by computer programs.

Organizations involved in frequent design of ribbon parachutes should establish these

programs.

7.4.10 Ribbon Parachute Canopies with Continuous Horizontal Ribbons

Ribbon parachute canopies are frequently designed and manufactured with continuous

horizontal ribbons either in single or two-section canopies. The continuous ribbon Jesign

decreases weight and volume, increases the strength of the horizontal ribbon-radial

connection, and simplifies manufacturing. Continuous horizontal ribbons change the porosity

characteristics of the canopy.

Figure 7-19 shows how the individual horizontal ribbons orient themselves in a canopy

manufactured from individual triangular gores. In the inflated canopy, the horizontal ribbons

in the canopy crown area orient parallel to the canopy design. However, in the skirt area, the

canopy design line is almost parallel to the airflow. This design, usually called the "venetian

blind effect," causes ti:e longer leading edge of each horizoatal ribbon to bulge out and

position the ribbon with a positive angle of attack to the airflow. The result is an increase in

effective porosity under high dynamic pressure conditions. The venetian blind effect is

discussed in section 6.2.4, and the influence of canopy loading on the change in effective

porosity is shown in Figure 6-24.

7-54

NWC TI1 6575

Designing canopies with continuous horizontal ribbons changes the venetian blind

effect. Returning to Figure 7.19, it is obvious that continuous horizontal ribbons in the canopy

skirt area do not bulge out since leading and trailing ribbon edges have the same length and do

not position themselves with an angle of attack to the airflow. However, in the crown area of the

canopy where each gore forms a triangle, the equal length of the leading and trailing ribbon

edges now gives each ribbon a negative angle of attack thereby increasing the effective porosity

in the canopy crown area. The effect is minimized by large number of gores arid by the use of a

center vertical ribbon, or a miniradial, as Sandia engineers call it.

Discussion with Sandia and industry personnel indicates that no measurable difference

has been found in the aerodynamic characteristics of ribbon parachute canopies designed

with individual gores or with continuous horizontal ribbons so long as the canopies contain a

large number of gores and a center vertical ribbon. However, a slight delay in initial inflation

seems to occur on small parachutes with a small number of gores. Closer spacing of vertical

ribbons in the canopy crown area should counteract this delay. Another method of

counteracting the delay is by gathering the trailing edges of horizontal ribbons with several

rows of stitching and using a lower porosity in the crown area.

7.4.11 Use of Kevlar Fabrics

Many modern ribbon parachutes use Kevlar suspension lines, risers, and canopy skirt,

lateral, and vent tapes, which results in a decrease in weight and volume. Section 6.5.5

discusses all aspects of working with Kevlar in the design of parachute assemblies. This

includes physical characteristics of Kevlar fibers and fabrics, available Kevlar fabrics, and

experience ;il designing in Kevlar. Section 6.6.5 should be studied before designing in Kevlar.