Parachute Performance: Difference between revisions
No edit summary |
|||
| Line 116: | Line 116: | ||
An increase in drag coefficient for a specific parachute can be accomplished by increasing the length of the suspension lines (see Figure 5-19). The increase in suspension-line length causes the parachute to open wider with a larger inflated area, <math>S_p</math>, and inflated diameter, <math>D_p</math>. The drag coefficient, <math>C_{D_p}</math> related to the inflated (projected) area, <math>S_p</math>, decreases slightly with an increase in line length and a related increase in projected diameter (see Figure 5-19b). However, the drag coefficient clearly increases with an increase in suspension-line ratio, <math>L_e/D_o</math> (Figure 5-19a). | An increase in drag coefficient for a specific parachute can be accomplished by increasing the length of the suspension lines (see Figure 5-19). The increase in suspension-line length causes the parachute to open wider with a larger inflated area, <math>S_p</math>, and inflated diameter, <math>D_p</math>. The drag coefficient, <math>C_{D_p}</math> related to the inflated (projected) area, <math>S_p</math>, decreases slightly with an increase in line length and a related increase in projected diameter (see Figure 5-19b). However, the drag coefficient clearly increases with an increase in suspension-line ratio, <math>L_e/D_o</math> (Figure 5-19a). | ||
[[File:FIGURE 5-19. Drag Coefficients, CDo and CDp; Canopy Area Ratio, SpSo; and Diameter Ratio, Dp9Do; as a Function of Suspension-Line Ratio, Le9Do for a 1-Meter-Diameter Model Parachute..jpg|center|thumb|591x591px|FIGURE 5-19. Drag Coefficients, <math>C_{D_o}</math> and <math>C_{D_p}</math>; Canopy Area Ratio, <math>S_p/S_o</math>; and Diameter Ratio, <math>D_p/D_o</math>; as a Function of Suspension-Line Ratio, <math>L_e/D_o</math> for a 1-Meter-Diameter Model Parachute.]] | [[File:FIGURE 5-19. Drag Coefficients, CDo and CDp; Canopy Area Ratio, SpSo; and Diameter Ratio, Dp9Do; as a Function of Suspension-Line Ratio, Le9Do for a 1-Meter-Diameter Model Parachute..jpg|center|thumb|591x591px|FIGURE 5-19. Drag Coefficients, <math>C_{D_o}</math> and <math>C_{D_p}</math>; Canopy Area Ratio, <math>S_p/S_o</math>; and Diameter Ratio, <math>D_p/D_o</math>; as a Function of Suspension-Line Ratio, <math>L_e/D_o</math> for a 1-Meter-Diameter Model Parachute.]] | ||
<math>D_p</math>. The drag coefficient, <math>C_{D_p}</math>, related to the inflated (projected) area, <math>S_p</math>, decreases slightly with an increase in line length and a related increase in projected diameter (see Figure 5-19b). However, the drag coefficient clearly increases with an increase in suspension-line ratio, <math>L_e/D_o</math> (Figure 5-19a). | |||
The slopes of the curves for area and projected diameter growth in Figure 5-19 indicate that using suspension-line ratios larger than 1.1 may have provided additional drag. | The slopes of the curves for area and projected diameter growth in Figure 5-19 indicate that using suspension-line ratios larger than 1.1 may have provided additional drag. | ||
These data were obtained in model tests with 1-meter (3.3-foot)-diameter parachutes. Reference 5.3 provides background on the tests. | These data were obtained in model tests with 1-meter (3.3-foot)-diameter parachutes. Reference 5.3 provides background on the tests. | ||
Figure 5-20 shows the possible increase in drag coefficient for line ratios, <math>L_e/D_o</math>, up to 2.0. Parachutes with no skirt restrictions, such as flat and conical circular parachutes, increase the drag coefficient up to line ratios of 2.0. Parachutes with skirt restrictions, such as extended skirts and hemispherical canopies, show little drag coefficient increase at line ratios above 1.1. The data in Figure 5-20, taken from United States, British, and German sources, show relatively good concordance. | |||
[[File:FIGURE 5-20. Variation of Drag Coefficient With Suspension-Line Ratio for Several Parachute Types..jpg|center|thumb|549x549px|FIGURE 5-20. Variation of Drag Coefficient With Suspension-Line Ratio for Several Parachute Types.]] | |||
Calculations indicate that line-length ratios above 1.5 may be detrimental because of the associated weight increase of the longer lines. Systems that employ parachutes in clusters or use first-stage drogue chutes require long risers. Parts of these risers may be replaced by longer suspension lines on the individual parachutes to increase parachute drag and decrease the required parachute diameter and parachute assembly weight. | |||
=== 5.2.2 Forebody Wake Effect === | |||
Parachutes are always used in connection with a forebody, such as a parachute jumper, an aircraft, a load platform, or an Apollo-type space capsule. Each forebody produces a wake | |||
that affects the parachute, depending on the relationship of the inflated parachute diameter, | |||
DP, to forebody diameter, DB, and the distance between the end of the forebody and the | |||
leading edge of the inflated parachute canopy. Figure 5-21 illustrates the drag loss. A cargo | |||
container descending on a 100-foot-diameter parachute produces little wake effect, because | |||
both the diameter ratio, Dp/DB, and the distance between the container and the leading edge of | |||
5-20 | the parachute, LT, are large. The inflated diameter of the Apollo drogue chute was smaller | ||
than the diameter of the Apollo spacecraft. The distance between the leading edge of the | |||
parachute and the rear of the spacecraft was kept to a minimum to save weight. Many | |||
parachute jumpers have experienced the failure of a spring-loaded pilot chute that was ejected, | |||
but then collapsed and fell back on the jumper because of the blanketing or wake effect of the | |||
jumper's body. 0 Tests conducted in the NASA and Wright Field vertical wind tunnels determined that for | |||
vertical descending bodies, the parachute should be ejected to a distance equivalent to more | |||
than four times-and preferably six times-the forebody diameter, into good airflow behind | |||
the forebody. Applying the six-forebody-diameter rule has been successful on Apollo and | |||
other programs. Ejecting the parachute from a horizontal attitude or sideways out of the | |||
forebody wake can provide good inflation with shorter forebody-to-parachute canopy | |||
distances. However, successful inflation with shorter distances should be proven in tests of the | |||
most unfavorable-not the most favorable--deployment conditions. | |||
Deploying a small parachute in the wake of a large forebody also causes considerable loss | |||
in parachute drag and may affect the stability of the parachute. Drag losses of up to 25% have | |||
been experienced in wind-tunnel and free-flight tests. Figure 5-21 presents parachute drag | |||
losses caused by forebody wake measured in wind-tunnel and free-flight tests. The two dotted | |||
lines (I in Figure 5-21) encompass parachute wake loss data measured in wind-tunnel tests by | |||
the University of Minnesota and the California Institute of Technology (Cal Tech) (References | |||
5.7 through 5.9). Superimposed on this wind-tunnel data are free-flight test results obtained on | |||
the reefed 16.5-foot-diameter Apollo command module drogue chute tested behind three | |||
different forebodies. This drogue chute was tested behind (1) an 11.9-foot, boilerplate | |||
command module (CM) (II in Figure 5-21), (2) a 5.8-foot-diameter parachute test vehicle | |||
(PTV) (III), and (3) a 36-inch-diameter instrumented cylindrical test vehicle (ICTV) (IV) | |||
0 5-21 | |||
NWC TP 6575 | |||
Op 1.0 "3"" | |||
0.9 | |||
LEGEND | |||
0.B FOREBODY CANOPY | |||
0.7 | |||
I-. 01 1.0 D8__ __ _ __ __ _ __ __ _ | |||
Z B0 I DATA FROM REFERENCES 5.3 TO 5.11 | |||
M 0.6 13 APOLLO DROGUE CHUTE BEHIND CM" = | |||
w In APOLLO DROGUE CHUTE BEHIND PTV"' = | |||
0 I APOLLO DROGUE CHUTE BEHIND ICTVIJ = | |||
I XS-2 DROGUE CHUTE, REF 5.11 = | |||
c 0 E SANDIA WIND TUNNEL TEST. REF 5.12 A £ | |||
ICD = PARACHUTE DRAG COEFFICIENT | |||
CD,,= DRAG COEFFICIENT WITH NO FOREBODY | |||
0.4I | |||
0 NEGATIVE \ BASE PRESSURE REGION | |||
2 4 6 8 10 12 14 15 16 18 20 | |||
RATIO, LT/DB | |||
_i SEE FIGURE 5-22 FOR DEFINITIONS. | |||
FIGURE 5-21. Parachute Drag Loss Caused by Forebody Wake. | |||
5-22 O | |||
NWC TP 6575 | NWC TP 6575 | ||
(Reference 5.10). These measured Apollo parachute data agree well with data from the | |||
University of Minnesota and the Cal Tech wind-tunnel tests. | |||
Parachute wake effect data measured in wind-tunnel tests behind a 3/8 scale model of the | |||
ejectable nose section of the XS-2 research aircraft (V)(Reference 5.11), and data measured on | |||
model parachutes by the Sandia National Laboratories (VI) (Reference 5.12), are included in | |||
Figure 5-21. | |||
Figure 5-22 details the measured forebody wake effect on the 16.5-foot-diameter ribbon | |||
drogue chute of the Apollo Command Module shown in Figure 5-21. | |||
Many forebodies, such as aircraft, have a noncylindrical cross section. Figure 5-23 | |||
demonstrates a method that has been used successfully to convert an odd-shaped cross section | |||
to a circular area. The area of the forebody, SB, included in the inflated area of the parachute | |||
behind the forebody is converted into the area of an equivalent circle. The diameter of this | |||
circle, DB, is then used as the reference forebody diameter. | |||
f | |||
140 I1.0 (C S)p | |||
0 1.0 1 _o | |||
DRAG 0 0.92 01 0 (CD S). | |||
AREA 120 - 01 0TCDs 0 0.82 08 | |||
100- 0 | |||
FOREBODY I | |||
5 | DIAMETER 11.9 5.8 3.0 | ||
(FT)- | |||
CONFIGURATION __ | |||
DESIGNATION 8/P CM PTV ICTV | |||
VHCE BOILERPLATE PRCUEINSTRUMENTED VHCE COMMAND PARAVEHCHUE CYLINDRICAL | |||
MODULE TETVHCETEST VEHICLE | |||
FIGURE 5-22- Drag Lous of the Apollo 16.5-Foot-Diameter, Ribbon | |||
Drogue Chute Caused by Different Forebodies. | |||
5- | <nowiki>*</nowiki> 5-23 | ||
NWC TP 6575 | NWC TP 6575 | ||
5.2.3 Measured Drag Coefficients of Various Types of Parachutes | -/ _ INFLATED PARACHUTE DIAMETER, D O | ||
EFFECTIVE FOREBODY AREA, SB | |||
EFFECTIVE FOREBODY DIAMETER, DB | |||
77, | |||
FIGURE 5-23. Determination of Effective Forebody Diameter. | |||
5.2.3 Measured Drag Coefficients of Various Types of Parachutes | |||
Drag coefficients are discussed in this section for solid flat, conical, triconical, | |||
extended-skirt, hemispherical, annular, and cross parachutes. These data were calculated | |||
from drop tests conducted over a period of time, primarily at the El Centro test facility. The | |||
main source for determining rates of descent were phototheodolite measurements, although | |||
some older tests used the 300-foot drop-line method. Most of the data were collected by the | |||
author; the summary data in Figure 5-24 were plotted by E. Ewing of Northrop-Ventura and | |||
presented in Figure 6-35 of Reference 2.1. | |||
Figure 5-24 plots the measured drag coefficient data for solid, flat circular, circular | |||
conical, triconical, extended-skirt, ringsail, annular, and ringslot parachutes. The data confirm | |||
the previously stated fact that triconical, annular, and extended-skirt parachutes have the | |||
highest drag coefficients. The data also confirm that, similar to model parachutes | |||
(Figure 5-16), the drag coefficients of unstable, large parachutes decrease with increasing rates | |||
of descent. | |||
References 5.13 through 5.20 refer to solid circular flat, circular conical, and triconical | |||
parachutes in general, and not to any specific parachute evaluated for the drag coefficient data | |||
in Figure 5-24. | |||
5-24 | 5-24 | ||
NWC TP 6575 | |||
0 | |||
1.1 | |||
"A A Av | |||
1-" 0.9 z | |||
U�LLU- 0.8__ | |||
0 | |||
" 0.7 | |||
0.6 | |||
0.5 - - | |||
15 20 25 30 35 40 50 60 70 80 90 | |||
RATE-OF-DESCENT, Veo FPS (EAS) | |||
PARACHUTE TYPE D0 . FT Le'Do | |||
<nowiki>*</nowiki> SOLID FLAT CIRCULAR 24-28 0.75-1.0 | |||
9 SOLID FLAT C!RrCtJLAR 100 0.95-1.0 | |||
V SOLID CONICAL CIRCULAR 95-100 0.95-1.0 | |||
A TRICONICAL 79.6-100 | |||
-- 14.3% EXTENDED SKIRT 60-67.3 0-92-1.0 | |||
" 10% EXTENDED SKIRT 56-67.2 1.0 | |||
10% EXTENDED SKIRT MC-1 35 0.85 | |||
" 10% EXTENDED SKIRT 34.5-38 0.87-0.94 | |||
"--@-RINGSAIL (XT = 7-8%) 56.2-84.2 0.94-0.97 | |||
-'•"RINGSAIL OT = 72%) 88.1 1.4 | |||
<nowiki>*</nowiki> ANNULAR (Dv/Dp = 0.63) 42-64 1.25 | |||
FIGURE 5-24. Drag Coefficient Versus Rate of Descent for Various Types of | |||
Solid Textile Parachutes. | |||
<nowiki>*</nowiki> 5-25 | |||
NWC TP 6575 | |||
Extended-Skirt Parachutes. Figure 5-25 shows the drag coefficient versus rate of descent 0 | |||
for various types of extended-skirt parachutes. These data are the result of numerous tests | |||
conducted with individual parachutes. The extended-skirt parachute was developed at | |||
5 | Lakehurst, New Jersey, by the U.S. Navy in the late 1940s (Reference 5.21). In 1952, the U.S. | ||
Air Force used the extended-skirt design to develop the T-10 Troop Parachute (Reference | |||
5.22). Extended-skirt parachutes designed for recovery of the Q-2 and the USD-5 drones | |||
achieved high drag coefficients combined with reasonably good stability of about 10 degrees of | |||
oscillation (References 5.23 and 5.24). | |||
1.0 | |||
0.1 94!tA..~ YBL TP | |||
C° LEGEND | |||
-"0SYMBOL TYPE REF | |||
Z 0.6 FT | |||
Ribbon Parachutes. Section 5.8contains drag data on ribbon parachutes for the subsonic and supersonic range. Ribbon parachute performance depends to a large extent on selection of the right porosity. Design data, including the required porosity for a particular parachute size and application, are discussed in Chapter 6. References 5.39 through 5.47, published by various organizations, discuss performance, design details, and subsonic and supersonic applications of ribbon parachutes. | 10% ES 38 5.23 L 10% ES 34.6 6.22 | ||
o 0.4 0 FES 71 5,23 U | |||
0 FES 78 523 | |||
A FES 67 5.24 | |||
0.2 0 FCES 28 5.2 | |||
A EXPER 36.4 5.2 | |||
0 10% ES 34.9 5.23 | |||
0.0I I | |||
10 16 20 25 30 35 40 45 | |||
RATE-OF-DESCENT. Veo FPS | |||
FIGURE 5-25. Drag Coefficient Versus Rate of Descent for Various | |||
Extended-Skin Parachutes. | |||
Combining the high drag effect of the triconical parachute with the good stability and low | |||
opening shock characteristics of the extended skirt design may produce a parachute | |||
combining the best features of both designs. | |||
The sensitivity of extended-skirt parachutes to suspension-line length is shown in | |||
Figure 5-26. These tests were conducted with an 11.8-foot-diameter, 10% extended-skirt | |||
parachute in the Wright Field vertical wind tunnel. The data also demonstrate the effect of | |||
velocity on the drag coefficient. | |||
Cross Parachute. In recent years, the cross parachute has been used for aircraft and | |||
ordnance deceleration as a low-cost replacement for the ringslot parachute. The cross | |||
parachute was first tested in 1947 by the Naval Ordnance Laboratory (Reference 5.25) and was | |||
reintroduced in 1%2 as the French cross parachute (References 5.26 and 5.27). The Naval | |||
Surface Warfare Center (NSWC) at Silver Spring, Md., has conducted many aerodynamic and | |||
5-26 0 | |||
NWC TP 6575 | |||
00 | |||
0.9- | |||
S0.85-- . . | |||
S0 Ve 20 FPS | |||
,0 /Ve = 30 FPS | |||
O 0.75. | |||
0.65,± | |||
'374 | |||
0.6 0.7 0.8 0.9 10 1.1 1.2 13 1.4 | |||
SUSPENSION-LINE-LENGTH RATIO, LeD 0 | |||
FIGURE 5-26. Effect of Suspension-Line Ratio on an | |||
1.8-Foot-Diameter Extended-Skirt Parachute. | |||
stress investigations on cross parachutes (References 5.28 to 5.32). NSWC is using the cross | |||
parachute for the stabilization and retardation of mines, see section 8.6.4. Reference 5.33 | |||
describes the use of a cross parachute as a final descent parachute. Figure 5-27 shows the cross | |||
parachute drag coefficient as a function of rate of descent evaluated from the NSWC | |||
programs. This stable parachute increascs its drag coefficient witl a decreasing rate of | |||
descent, a fact previously observed only on unstable parachutes. Drag znd stability of the cross | |||
parachute depend on the arm's diameter-to-width ratio (W/L), on the number and length of | |||
suspension lines, and on cloth porosity. To conform togeneral use, the nominal diameter, Do, is | |||
used in this manual instead of the arm length to define cross parachute diameter. Reports | |||
published primarily by the NSWC should be consulted before using this parachute. | |||
Wind-tunnel and water-tank tow tests on cross parachutes were conducted by the University of | |||
Leicester, England (Reference 5.34 and 5.35). | |||
Annular Parachute. The annular parachute was developed in 1947 and named the airfoil | |||
parachute (Reference 5.36). Figure 5-28 shows its high drag coefficient. The parachutes with | |||
individual symbols in the figure are annular parachutes used in connection with a ringslot or | |||
ringsail engagement parachute for midair retrieval systems (References 5.37 and 5.38). | |||
Ribbon Parachutes. Section 5.8contains drag data on ribbon parachutes for the subsonic | |||
and supersonic range. Ribbon parachute performance depends to a large extent on selection of | |||
the right porosity. Design data, including the required porosity for a particular parachute size | |||
and application, are discussed in Chapter 6. References 5.39 through 5.47, published by | |||
various organizations, discuss performance, design details, and subsonic and supersonic | |||
applications of ribbon parachutes. | |||
5-27 | 5-27 | ||
NWC TP 6575 | |||
0.8 -9--o I® 1* * | |||
0( 0 LD3 | |||
8 o.5 | |||
<nowiki>L~~~ 10"....</nowiki> | |||
Z 0.6 FL /o - - - I | |||
_____ LEGEND | |||
TYPE Do, REFERENCE o SYMBOLS TEST FT | |||
0.2 (0) 0 FFT 136 526 | |||
Q -- WTT 2.5 5 28/29 | |||
@ WTT 2.5 5.27 | |||
) FFT 613 5.33 | |||
0 _--1. 1 | |||
10 20 30 40 50 60 70 80 | |||
RATE -OF-DESCENT. V FPS | |||
FIGURE 5-27. Drag Coefficient Versus Rate of Descent for Various Cross Parachutes. | |||
12 | |||
<nowiki>*</nowiki>0 | |||
L) =LEGEND | |||
0 SYMBOL O0 TYPE REF | |||
< ~OF E oFT TEST | |||
06 28 FFT 53•6 | |||
0 42 FFT 537 | |||
718 FFT 638 | |||
S • 84 FFT 67 FFT - | |||
0 1o 15 20 25 30 | |||
RATE -OF-DESCENT. Vo FPS 0 | |||
FIGURE 5-28. Drag Coefficient Versus Ratc of Dcscent for Various | |||
Annular Parachutes. | |||
5-28 | |||
NWC TP 6575 | |||
"The influence of Mach number on the drag of ribbon-type drogue chutes is discussed in | |||
section 5.8. | |||
Ringslot Parachutes. References 5.48 and 5.49 give design details on ringslot parachutes. | |||
A drag coefficient, CD0o, of 0.65 has been measured in free-fall tests. Selection of the proper | |||
total porosity, in accordance with Chapter 6, is important. Ringslot parachutes used as landing | |||
deceleration parachutes for aircraft experience a drag coefficient reduction from 0.65 to 0.60 | |||
because of the large wake behind the aircraft. | |||
Rlngsail Parachutes. Reference 5.50 is a summary report on ringsail performance, | |||
design, and application. These parachutes were used as the main descent parachutes for the | |||
Mercury, Gemini, and Apollo spacecraft and for the ejectable crew module of the F-ill | |||
aircraft. | |||
Hemisflo Parachute. This supersonic ribbon parachute should be used at speeds of | |||
Mach 2 or higher. References 5.51 and 5.52 provide information on the development, design, | |||
and application of hemisflo parachutes. | |||
Guide Surface Parachute. This parachute was developed as a high-stability, low drag | |||
parachute for the stabilization of bombs, mines, and torpedoes. It combines good stability | |||
with excellent damping characteristics. For details see References 5.53 and 5.54. | |||
Disk-Gap-Band Parachute. Some information on this parachute, used successfully to | |||
land the Viking spacecraft on the planet Mars, is contained in References 5.55 and 5.56. | |||
Rolating Parachutes. Several types of rotating parachutes have been used successfully. | |||
Angled vents in the parachute canopy rotate the parachute. Centrifugal forces acting on the | |||
canopy and suspension lines increase the projected diameter, resulting in a high drag | |||
coefficient. Attempts to use rotating parachutes with diameters greater than 10 feet have been | |||
unsuccessful because of deployment and canopy wrap-up problems. References 5.57 through | |||
5.59 provide information on the three best known types of rotating parachutes. | |||
Maneuverable (Gliding) Parachutes. Maneuverable gliding parachutes and their | |||
performance characteristics are discussed in section 5.9. | |||
Balloon-'yype Decelerators. These deceleration devices, including the Goodyear ballute, | |||
are discussed in section 5.8. | |||
5.2.4 Effect of Reynolds Number on Parachutes | |||
Chapter 4 states that parachutes, unlike airfoils, operate in turbulent flow because of the | |||
separation of the airflow at the leading edge of the parachute canopy. For this reason, the | |||
5-29 | 5-29 | ||
| Line 226: | Line 676: | ||
NWC TP 6575 | NWC TP 6575 | ||
Reynolds number does not appear to change the drag coefficient of parachutes. Measured data on parachute drag coefficient versus Reynolds number are compared in Figure 5-29 with the known Reynolds number effect on the drag coefficient of a sphere. These data are taken | Reynolds number does not appear to change the drag coefficient of parachutes. Measured | ||
data on parachute drag coefficient versus Reynolds number are compared in Figure 5-29 with | |||
the known Reynolds number effect on the drag coefficient of a sphere. These data are taken | |||
from Reference 2.1. | |||
S~CIRCULAR DISC | |||
Stability may be viewed as the tendency of a body to return to a position of balance or equilibrium after a displacement from that | 0 CIRCULAR DISC | ||
C RIGID HEMISPHERICAL | |||
Z ^. FABRIC HEMISPHERICAL | |||
",' 3 1 CRUCIFORM | |||
0• 3.79:1 CRUCIFORM | |||
SPH-ERE | |||
105 106 | |||
Re - vD i - | |||
FIGURE 5-.19. Effect of Reynolds Number on Drag Coefficient for a | |||
Sphere and Various Parachutes. | |||
5.3 STABILITY OF PARACHUTE SYSTEMS | |||
5.3.1 General Definition | |||
Stability may be viewed as the tendency of a body to return to a position of balance or | |||
equilibrium after a displacement from that pe.sition. Controllability may be defined as the ease | |||
of causing that movement, or as the effectiveness of the mechanism us,,ed to cause the body to | |||
return to its original position. Various concepts of stability can be illustrated by simple | |||
examples. In Figure 5-30a, a ball is shown at rest in a concave depression. A displacement of | |||
the ball will result in gravity restoring it to its original position. This state is called "stable." If | |||
the ball is placed on a flat surface. a displacement of the ball from its position of rest will cause | |||
the ball to come to Test at a different location on the flat plate, with no tendency for the ball to | |||
return to its original position; this state is termed "neutrally stable" (Figure 5-30b). | |||
Figure 5-30c shows a ball placed in a state of equilibrium atop a larger spherical ball. Clearly, | |||
any displacement of the small ball on the large sphere causes the ball to continuously move | |||
away from its original position of stability. This condition is termed "unstable." In the three | |||
simpie examples, we have considered the conditions connected with static stability. | |||
5-30 | 5-30 | ||
NWC TP 6575 | |||
(a) STABLE (b) NEUTRALLY STABLE (c) UNSTABLE | |||
FIGURE 5-30. Illustration of Static Stability. | |||
Dynamic stability refers to the continued motion of a moving body and may be illustrated | |||
by considering the ball on the concave surface in Figure 5-30a. The friction forces on the ball | |||
are always in a direction opposite to its motion. The friction forces, positive damping effect, | |||
together with the gravity component, make the ball tend to oscillate with a decreasing | |||
amplitude until it finally achieves the illustrated position of static stability. A ball in this | |||
dynamic environment is called "dynamically stable." If the aerodynamic forces of air | |||
resistance and the mechanical frictional forces could be reduced to zero-an impossible | |||
condition-there would be no damping force on the ball, and a small displacement of the force | |||
applied to the ball would cause an indefinite oscillation of constant amplitude. Such a | |||
condition is termed "neutrally dynamically stable." If friction force is overcome by some | |||
external force-for example, a propulsion force-the ball would oscillate with an increasing | |||
amplitude and would not return to its position of equilibrium; this condition is called | |||
"dynamically unstable." | |||
These conditions of dynamic stability are graphically illustrated in Figure 5-31, which | |||
demonstrates the stability of three bodies. Body "a" is dynamically and statically unstable. | |||
Body "b" is statically stable but dynamically unstable, resulting in ever-increasing oscillations. | |||
Body "c" is dynamically and statically stable, resulting in oscillations dampened with time. | |||
The fact that a body is statically and dynamically stable is frequently not sufficient. For | |||
example, an automobile without shock absorbers is statically and dynamically stable in its | |||
spring motions, but may provide an uncomfortable ride because of insufficient damping of its | |||
body oscillations. Installation of shock absorbers increases positive damping and causes a | |||
rapid decrease of the body oscillations with time, thereby providing a comfortable ride. | |||
5-31 | 5-31 | ||
NWC TP 6575 | |||
z | |||
0 | |||
t a | |||
Stability is defined as the tendency of a body to return to a position of equilibrium after displacement. Parachute engineers frequently use the term stability loosely. If two airdrop platforms descend, each on a 100-foot-diameter parachute, and one parachute oscillates * 30 degrees and the other ± 5 degrees, observers frequently call the former parachute system unstable and the latter stable. In reality, both parachute systems are statically unstable in the oscillating mode but are sufficiently dampened dynamically to stay within their ranges of oscillation without increasing the oscillation amplitude. It is more precise to define these parachutes as oscillating ±30 degrees or ± 5 degrees; and, if possible, to state that | 0 | ||
•5_b =e STBEUSAL | |||
2 TIME 0 | |||
U. \Z | |||
W STATICALLY DYNAMICALLY | |||
a = UNSTABLE UNSTABLE | |||
b - STABLE UNSTABLE | |||
c = STABLE STABLE | |||
FIGURE 5-31. Graphical Illustration of Dynamic Stability. | |||
A statically stable parachute may require excessive time to decrease its oscillation after | |||
an external disturbance, such as a wind gust, indicating that the parachute's damping | |||
characteristics are inadequate for stabilizing an unstable body. | |||
In the case of an aircraft, good static and dynamic stabilities are desirable for large | |||
cargo-type aircraft, but this stability counteracts fast changes in attitude and position required | |||
for fighter aircraft, which are generally built with low or neutral static stability. In recent years, | |||
aircraft requiring a high degree of mobility have been designed with a slightly negative static | |||
stability, thus increasing mobility and decreasing the size and drag of the control surfaces. | |||
S.3.2 Parachute Stability | |||
Stability is defined as the tendency of a body to return to a position of equilibrium after | |||
displacement. Parachute engineers frequently use the term stability loosely. If two airdrop | |||
platforms descend, each on a 100-foot-diameter parachute, and one parachute oscillates * 30 | |||
degrees and the other ± 5 degrees, observers frequently call the former parachute system | |||
unstable and the latter stable. In reality, both parachute systems are statically unstable in the | |||
oscillating mode but are sufficiently dampened dynamically to stay within their ranges of | |||
oscillation without increasing the oscillation amplitude. It is more precise to define these | |||
parachutes as oscillating ±30 degrees or ± 5 degrees; and, if possible, to state that | |||
5-32 | 5-32 | ||
| Line 260: | Line 854: | ||
NWC TP 6575 | NWC TP 6575 | ||
disturbances such as those caused by wind gusts are dampened within a given number of full oscillations. The parachute oscillating | 0 disturbances such as those caused by wind gusts are dampened within a given number of full | ||
oscillations. The parachute oscillating + 5 degrees most likely meets the requirements for | |||
airdrop; however, the same parachute is unsuitable for stabilizing airdropped bombs or | |||
torpedoes. For this application, a parachute with zero oscillation and good damping is | |||
required. As defined later in this section, a parachute meeting this requirement has a steep | |||
negative dC./dc over a wide range of angles of attack. | |||
Why should one parachute have no oscillation and strong damping characteristics while | |||
another parachute oscillates violently? Figure 5-32 explains this difference by showing the | |||
airflow around several types of parachute canopies and rigid hemispheres. The airflow, made | |||
visible with smoke ejected from equally spaced nozzles in front of the parachute models, acts | |||
as streamlines, as explained in Chapter 4. Figure 5-32a shows the airflow around an imporous | |||
hemisphere. Airflow cannot get through the canopy but goes around and separates on the | |||
leading edge of the hemisphere in alternating vortexes, forming what is called the Karman | |||
<nowiki>--------------------------</nowiki> / ,- | |||
KARMAN VORTEX | |||
TRAIL | |||
-- . .... M- ---(SOLID CIRCULAR)_ | |||
N 8 | |||
ATTACHED FLOW IN | |||
(A) IMPOMOUS CANOPY. INSTAGILITY CAUSRO 9V SIDE PONCI. N. ft | |||
FLOW SEPARATION (d) POAOUSCANOPY. STABILIZING MOMENT, 0 * A * N ft * | |||
.2 • UNIFORM | |||
- . .. --. , WAKE LARGE PROJECTED AREA _ (RIBBON) | |||
FLOW SEPARATION DRAG 0 | |||
(I) POROUS CANOPY. NO SDoE FORC1. NO UN&TAILE MOMCMT. -A | |||
•_ FLIOý% SEPARATION M) CANOPY WITH SCOIAMAAION 9001, STAWlLIZlNO MOhMINT, | |||
-FLOVV SEPARATION | |||
Ic) CANOPY WITN SEPARATION LOGE (OGUIOD URFAC1). | |||
No SIOID POAC. NO UNITABLe MOMENT. | |||
FIGURE 5-32 Relationship of Airflow and Stability for Various Parachutes. | |||
5-33 | 0 5-33 | ||
NWC TP 6575 | NWC TP 6575 | ||
Vortex Trail. The separation causes alternate pressure areas on opposite sides of the canopy, | |||
and these pressure areas produce the parachute's oscillations. | |||
Figure 5-32b shows the effect of openings in the canopy. Part of the air flows through the | |||
canopy and forms a uniform wake consisting of small vortexes. In addition, the airflow | |||
separates uniformly around the leading edge of the canopy, eliminating the destabilizing | |||
alternate flow separation of the Karman Vortex Trail. Uniform wake and airflow separation is | |||
the principle of the ribbon parachute and all slotted parachute canopies. | |||
The guide surface parachute (Figure 5-32c) has a sharp separation edge around the skirt | |||
of the canopy, creating a strong, uniform airflow separation around the leading edge. In | |||
addition, the inverted leading edge (guide surface) creates a large, stabilizing normal force. | |||
Both the normal force, N, and the drag force, D, create a stabilizing moment if the parachute is | |||
displaced from its zero-angle-of-attack position (Figure 5-32e). The known main design | |||
features for creatingstable parachutes are uniform airflow separation around the leading edge | |||
of the canopy, airflow through the canopy, and a large restoring moment such as that generated | |||
by a guide surface. | |||
The static stability of various parachutes has been measured numerous times in | |||
wind-tunnel tests. Figure 5-33 plots the moment coefficient of several parachute types and of | |||
rigid hemispheres, as measured by the University of Minnesota (References 5.60 and 5.61). A | |||
negative dCm/da of the moment coefficient curve indicates that the parachute is stable and | |||
will return to its zero-angle-of-attack position after a disturbance. The solid, flat. circular | |||
5-34 | canopy is a typically unstable parachute. It will oscillate between k 25 degrees, but if deflected | ||
more than 25 degrees it will return to the 25-degree position. The ribbon and guide surface | |||
parachutes will return to their zero-angle-of-attack attitude if displaced, as indicated by the | |||
negative slope of the dCm/dct curve going through the zero-angle-of-attack position for both | |||
parachute types. | |||
The guide surface parachute has the steepest dCm/dc, and, therefore, the strongest | |||
stabilizing moment and best damping characteristics of all known parachutes. | |||
Larger parachutes oscillate less than small parachutes. A 3-foot-diameter solid flat | |||
circular parachute manufactured from standard 1.1-oz/y 2 ripstop material, tested in a wind | |||
tunnel, will oscillate about ± 35 to 40 degrees. The standard 28-foot-diameter personnel | |||
parachute oscillates about ± 30 to 35 degrees. The 100-foot-diameter G-11 cargo parachute | |||
oscillates about 10 to 20 degrees. The 200-foot-diameter cargo parachute manufactured from | |||
1.6-oz/y 2 material with about the same porosity as the other parachutes (described in | |||
Reference 5.14) oscillates less than 5 degrees. Ludtke discusses oscillation problems in | |||
Reference 5.62. | |||
5-34 0 | |||
NWC TP 6575 | NWC TP 6575 | ||
5-35 | RIGID HEMISPHERE WITH | ||
35% GEOMETRIC POROSITY | |||
0.4 | |||
GUIDE SURFACE PARACHUTE | |||
NOMINAL POROSITY: | |||
100 FT 3 /FT 2 /MIN | |||
0.3 | |||
E | |||
1-: 0.2 SOLID FLAT PARACHUTE | |||
Z NOMINAL POROSITY: | |||
2_ 100 FT 3 | |||
/FT 2 /MIN | |||
U. | |||
ILLU | |||
0 | |||
L) 0.1 | |||
I�z | |||
0 | |||
+ | |||
RIGID HEMISPHERE | |||
0.1 NONPOROUS RBO AAHT | |||
Cm RELATED TO PROJECTED 28%BO GEMERICALT | |||
AREA AND MOMENT CENTER POROSITY | |||
1.33 D P BELOW CANOPY SKIRT | |||
I I I I I I I I I 1 | |||
-70 -60 -50 -40 -30 -20 -10 +10 +20 +30 +40 +50 | |||
ANGLE OF ATTACK,a, DEGREES | |||
NOTE: IN THE U.S. A STABILIZING MOMENT IS DEFINED | |||
AS HAVING A NEGATIVE dCm/da. IN EUROPE, A | |||
STABILIZING MOMENT IS DEF:NED AS HAVING | |||
A POSITIVE dCm/da. | |||
FIGURE 5-33. Moment Coefficients Versus Angle of Attack for Guide Surface; Ribbon; | |||
and Flat, Circular Parachutes; and for Porous and Nonporous Hemispheres. | |||
0 5-35 | |||
NWC TP 6575 | NWC TP 6575 | ||
5.3.3 Stability of a Parachute Body System | 5.3.3 Stability of a Parachute Body System | ||
Parachutes that are used with stable air vehicles must also be stable and not interfere | Parachutes that are used with stable air vehicles must also be stable and not interfere | ||
with the inhercnt stability of the vehicle. Parachutes with good stability and high drag are used, | |||
such as the ribbon, ringslot, and cross parachutes. If a fast-falling, unstable body must be | |||
stabilized while maintaining a high rate of descent, a parachute with a strong negative | |||
dCm/do,, such as a guide surface parachute, may be preferable. For each parachute assembly, | |||
a compromise between required stability, weight, volume, and cost determines the final | |||
selection. | |||
The following parachute application ranges have been established based on many years | |||
of practical experience. | |||
Aircraft Landing Deceleration. Aircraft are inherently stable and do not require aircraft | |||
landing deceleration parachutes to contribute to their stability. Therefore, high drag stable | |||
parachutes that do not interfere with the aircraft controllability are used. Ribbon, ringslot, and | |||
5-36 | cross parachutes are used primarily for aircraft landing deceleration. | ||
Bomb Stabilization. During World War II, the Germans developed parachute-stabilized | |||
bombs that enabled them to shorten the length of the bomb and to store more bombs in | |||
existing aircraft bomb bays. These fast-falling bombs required a low drag, highly stable | |||
parachute with good damping capability to obtain the desired stability. The guide surface | |||
parachute was developed specifically for this application as a low drag, high-stability | |||
parachute (Reference 5.53). A single riser attachment did not provide a sufficiently stable | |||
parachute-bomb system, and a more rigid connection between the bomb and the parachute | |||
was required. Figure 5-34 contains two examples of rigid parachute-bomb connections: the | |||
multiple-point attachment on the circumference of the bomb and the geodetic attachment. | |||
The geodetic attachment is the best solution but is more complex. | |||
Torpedo and Mine Stabilization. Mines and torpedoes that are airdropped from low | |||
altitudes are equipped with retardation parachutes to | |||
1. Decelerate the store to an acceptable water entry velocity, generally below 200 ft/s. | |||
2. Obtain a water entry angle that avoids ricochet. | |||
3. Avoid store oscillation and associated store damage at water impact. | |||
Guide surface, ribbon, ringslot, and cross parachutes are being used successfully for this | |||
application. | |||
Bomb Retardation. Bombs dropped at high speeds from low-flying aircraft must be | |||
retarded to | |||
1. Obtain a steep impact angl, to avoid ricochet. | |||
2. Permit the aircraft to escape the effective range of the exploding bomb. | |||
3. Obtain a good fragmentation pattern associated with a steep impact angle. | |||
5-36 0 | |||
NWC TP 6575 | NWC TP 6575 | ||
5-37 | S | ||
BOMBS | |||
(a) SINGLE POINT (b) MULTIPLE POINT (c) GEODETIC | |||
<nowiki>*</nowiki> AIRCRAFT CREW MODULES | |||
(d) CENTER LINE (e) MULTIPLE POINT (f) SINGLE POINT | |||
CG ATTACHMENT CG ATTACHMENT | |||
FIGURE 5-34. Various Conrigurations of Parachute Vehicle Attachments. | |||
5 5-37 | |||
NWC TP 6575 | NWC TP 6575 | ||
Stable parachutes with good drag characteristics used for this one-time application include ribbon, ringslot, and cross parachutes as well as the inflatable ballute-type retarders. | Stable parachutes with good drag characteristics used for this one-time application | ||
include ribbon, ringslot, and cross parachutes as well as the inflatable ballute-type retarders. | |||
Fjection Seat, Encapsulated Seat, and Crew-Module Stabilization and Retardation. All | |||
three aircraft escape systems need parachutes for stabilization and retardation. Stabilization | |||
is required in pitch, yaw, and roll; parachutes can provide stabilization in pitch and yaw, but | |||
are poor for roll control. For descent from a high altitude, a roll control of not more than 2 to 3 | |||
rpm is necessary for aviator comfort. This control can be obtained with a relatively large | |||
drogue chute with an equivalent sea-level rate of descent of 120 to 150 ft/s. | |||
The aircraft crew-module stabilization in Figure 5-34 demonstrates the problem of | |||
stabilizing an asymmetrical body with the center of gravity (CG) off the center line of the | |||
vehicle. In the example shown, the drogue chute had to be attached offset to the nose section of | |||
the XS-2 research aircraft to ensure that the parachute force line would run through the CG of | |||
the crew module with the module hanging at a -2 degree zero lift attitude to eliminate | |||
destabilizing side forces (Reference 5.11). | |||
The stability relationship of parachute and forebody is quite complex in systems where | |||
unstable forebodies must be stabilized by minimum size parachutes. Both the forebody and | |||
the parachute can oscillate in a 360-degree plane. The stability of such two-body, | |||
multi-degree-of-freedom systems has been investigated by several authors (References 5.63 | |||
through 5.67). | |||
Neustadt showed that deploying a parachute opposite the oscillating motion of the | |||
forebody may increase the parachute force by as much as 20% (Reference 5.68). | |||
S.4 PARACHUTE INFLATION PROCESS | |||
5.4.1 Opening Force Investigations | 5.4.1 Opening Force Investigations | ||
Many attempts have been made to develop theoretical solutions to the parachute inflation process and obtain quantitative values for opening time and force. Investigations by Mueller, Scheubel, O'Hara, Rust, Heinrich, Wolf, and Purvis, defined in References 5.69 through 5.75, have increased the understanding of the parachute opening process, including the effect of apparent mass. However, no satisfactory practical solution for calculating filling time and parachute opening forces has evolved. The analytical solution of the opening process has been complicated in recent years by the development of means for controlling parachute inflation, such as reefing, sliders for steerable parachutes, pull-down vent lines, and related devices. While these methods provide control of parachute inflation, and thereby the opening forces, they also interfere with the parachute's natural inflation process. A good account of the present status of the parachute inflation theory was presented by D. Wolf in 1982 during the University of Minnesota Short Course on Parachute Systems Technology (Reference 2.17). | Many attempts have been made to develop theoretical solutions to the parachute | ||
inflation process and obtain quantitative values for opening time and force. Investigations by | |||
Mueller, Scheubel, O'Hara, Rust, Heinrich, Wolf, and Purvis, defined in References 5.69 | |||
through 5.75, have increased the understanding of the parachute opening process, including | |||
the effect of apparent mass. However, no satisfactory practical solution for calculating filling | |||
time and parachute opening forces has evolved. The analytical solution of the opening process | |||
has been complicated in recent years by the development of means for controlling parachute | |||
inflation, such as reefing, sliders for steerable parachutes, pull-down vent lines, and related | |||
devices. While these methods provide control of parachute inflation, and thereby the opening | |||
forces, they also interfere with the parachute's natural inflation process. A good account of the | |||
present status of the parachute inflation theory was presented by D. Wolf in 1982 during the | |||
University of Minnesota Short Course on Parachute Systems Technology (Reference 2.17). | |||
5-38 | 5-38 | ||
NWC | NWC T? 6575 | ||
In 1942 Pflanz developed a numerical method for calculating parachute opening forces | |||
(References 5.76 and 5.77). He assumed that the drag area of the parachute or of any drag | |||
device increased from a low value to 100% in a given time and in a mathematically definable | |||
form, such as convex, concave, or linear. The parachute filling distance was assumed to be | |||
constant for a specific parachute. The Pflanz method includes altitude effects but does not | |||
include gravity effects or drag area overshoot after full opening. | |||
Schuebel was the first to investigate the effect of the apparent mass on the parachute | |||
opening process. He defined apparent mass as both the air mass inside the inflating canopy | |||
and the air mass outside the canopy that is affected by the inflation process (Reference 5.70). | |||
Modern, high-speed computers make it possible to calculate the time-dependent | |||
force-velocity-trajectory history of the parachute opening process for complex recovery | |||
systems. This calculation was first accomplished in 1960 by Space Recovery Systems, Inc. | |||
(Reference 5.23). The computer results agreed well with the forces measured in free-flight tests. | |||
This force-velocity-trajectory approach was used in an extended form for predicting the | |||
parachute opening forces of the Gemini and Apollo drogue and main parachutes (References | |||
5.78 and 5.79). McEwen gives an excellent review of previous efforts and recommends that | |||
inflation distance, not inflation time, be used as the reference for the inflation process. | |||
For a parachute-vehicle system moving in space (Figure 5-35), the trajectory equations | |||
can be written in the form shown in the figure. | |||
dv -F-Dr +Wv SINO | |||
dt My | |||
dO -g COS 0 | |||
dt V | |||
(F + DO) | |||
FIGURE 5-35. Angle and Force Relationships for a Deceleration | |||
System Moving in Space. | |||
The parachute force, F, as a function of time is | The parachute force, F, as a function of time is | ||
(m + m p)4 dv - +v- dm, + WvsinO | |||
(CDS)pp/2v 2 + -mp) | |||
5-39 | 5-39 | ||
| Line 362: | Line 1,292: | ||
NWC TP 6575 | NWC TP 6575 | ||
where | |||
F - parachute force acting parallel to the flight trajectory, lb | |||
D, - drag of the vehicle (payload), lb | |||
Wv - weight of the vehicle or payload, lb | |||
0 - trajectory angle against the horizontal, degrees | |||
S - deceleration of gravity, ft/s2 | |||
(CDS)p - parachute drag area, ft2 | |||
p - density of air, slugs/ft3 | |||
v = trajectory velocity, ft/s | |||
ma - apparent mass (added mass), slugs | |||
mp = mass of parachute, slugs | |||
mv - mass of the vehicle or payload, slugs | |||
Wp = weight of the parachute, lb | |||
The drag of the vehicle, Dr, depends on the drag area of the vehicle and on the | |||
instantaneous dynamic pressure, which changes during the opening process of the parachute. | |||
The trajectory angle, 0, changes from the launch or deployment angle to vertical most | |||
rapidly during and after urachute inflation. | |||
Changes in the value of the acceleration of gravity, g, do not affect the outcome at | |||
altitudes below 100,000 feet. | |||
The parachute drag area, (CDS) | The parachute drag area, (CDS)p, increases from close to zero at line stretch to 100% at | ||
full open canopy. | |||
The apparent or added mass, ma, is calculated by multiplying volume by density and by a form factor that depends on the particular parachute type. The apparent mass at an altitude of 40,000 feet is only one-quarter of the apparent mass at sea level, because apparent mass depends on density. Therefore, the apparent mass affects the magnitude of the parachute opening force at a given altitude. | Density, p, changes with altitude; this change must be considered for longer trajectories. | ||
Both parachute and payload are assumed to have the same velocity and the same trajectory | |||
angle. | |||
The apparent or added mass, ma, is calculated by multiplying volume by density and by a | |||
form factor that depends on the particular parachute type. The apparent mass at an altitude of | |||
40,000 feet is only one-quarter of the apparent mass at sea level, because apparent mass | |||
depends on density. Therefore, the apparent mass affects the magnitude of the parachute | |||
opening force at a given altitude. | |||
5-40 | 5-40 | ||
| Line 404: | Line 1,354: | ||
NWC TP 6575 | NWC TP 6575 | ||
In the parachute force equation, the vehicle weight is | 0 In the parachute force equation, the vehicle weight is Wv • sin 0. Using the sign | ||
convention of Figure 5-35, a parachute opening in a vertical attitude will have a force that is one | |||
unit weight higher than the force of a parachute opening in a horizontal attitude. This force | |||
difference must be considered in planning parachute test programs. | |||
5.4.2 Parachute Canopy Inflation | |||
Parachute inflation is defined as the time interval from the instant the canopy and lines | |||
are stretched to the point when the canopy is first fully inflated. Figure 5-36 shows the phases of | |||
canopy inflation. The canopy filling process begins when canopy and lines are stretched and | |||
when air begins entering the mouth of the canopy (a). After the initial mouth opening, a small | |||
ball of air rushes toward the crown of the canopy (b). As soon as this initial air mass reaches the | |||
vent (c), additional air starts to fill the canopy from the vent toward the skirt (d). The inflation | |||
process is governed by the shape, porosity, and size of the canopy and by air density and | |||
velocity at the start of inflation. Inflation is slow at first but increases rapidly as the mouth inlet | |||
of the canopy enlarges (e) and the canopy reaches its first full inflation (f). Most solid textile | |||
canopies overinflate and partially collapse because of the momentum of the surrounding air | |||
(g). Several factors contribute to an orderly, repeatable inflation process and to a low, uniform | |||
(a) OPENING OF CANOPY MOUTH | |||
<nowiki>*</nowiki> (b) AIR MASS MOVES ALONG CANOPY | |||
S(c) AIR MASS REACHES CROWN OF CANOPY | |||
(d) INFLUX OF AIR EXPANDS CROWN | |||
(TYPICAL REEFED INFLATION SHAPE) | |||
(e) EXPANSION OF CROWN RESISTED BY | |||
STRUCTURAL TENSION AND INERTIA | |||
if) CANOPY REACHES FIRST FULLY INFLATED | |||
STAGE | |||
5-41 | (g) SKIRT OVER-INFLATED, CROWN DEPRESSED | ||
BY MOMENTUM OF SURROUNDING AIR MASS | |||
FIGURE 5-36. Parachute Canopy Inflation Process. | |||
0 5-41 | |||
NWC TP 6575 | NWC TP 6575 | ||
opening force. The amount of air moving toward the canopy vent at point (b) should be small to | opening force. The amount of air moving toward the canopy vent at point (b) should be small to | ||
avoid a high-mass shock when the air bubble hits the vent of the parachute. The inflation of the | |||
canopy should occur axisymmetrically to avoid overstressing individual canopy parts. | |||
Overinflation of the canopy after the first initial opening should be limited to avoid delay in | |||
reaching a stable descent position. | |||
Methods have been developed to control the inflation of the canopy; the most frequently | |||
5-42 | used is canopy reefing. Reefing stops the inflation of the canopy at one or more steps between | ||
stages (c) and (0), thereby limiting the parachute opening force to a preselected level. | |||
Retfing is also required for uniform inflation of parachutes in a cluster. Stopping the | |||
inflation of all cluster parachutes at a point close to stage (d) of Figure 5-36 allows all | |||
parachutes to obtain an initial uniform inflation-a prerequisite for a uniform final | |||
inflation--without running into a lead/lag chute situation with widely varying parachute | |||
forces. Other means for controlling the parachute opening include ballistic spreader guns, | |||
sliders for gliding parachutes, and pull-down vent lines. | |||
5.4.3 Canopy Inflation Time | |||
Knowledge of the canopy filling time, defined as the time from canopy (line) stretch to the | |||
first full open canopy position, is important. Mueller and Scheubel reasoned that, based on the | |||
continuity law, parachutes should open within a fixed distance, because a given conical column | |||
of air in front of the canopy is required to inflate the canopy (References 5.69 and 5.70). This | |||
fixed distance is defined as being proportional to a parachute dimension such as the nominal | |||
diameter, DO. This assumption was reasonably confirmed in early drop tests with ribbon | |||
parachutes. French and Schilling, in papers published in 1968 and 1957, confirmed this | |||
assumption (References 5.80 and 5.81). Using the fixed-distance approach and the definitions | |||
in Figure 5-37, the filling distance for a specific parachute canopy can be defined as | |||
sf = n Dp - constant. | |||
With sf = n DP` the canopy filling time, tf, can be defined as shown in Figure 5-37. | |||
sf = n D P | |||
FIGURE 5.37. Filling Distance of a Parachute Canopy. | |||
5-42 0 | |||
NWC TP 6575 | NWC TP 6575 | ||
Because the parachute diameter, Dp, is variable, the fixed nominal diameter, Do, is used to calculate canopy filling time | Because the parachute diameter, Dp, is variable, the fixed nominal diameter, Do, is used | ||
to calculate canopy filling time | |||
n D. | |||
V | |||
where | where | ||
Do is the nominal | Do is the nominal par,,iiute diameter, feet | ||
v is the velocity at line stretch, ft/s | v is the velocity at line stretch, ft/s | ||
n is a constant, typical for each parachute type, indicating the filling distance as a multiple of Do , dimensionless. | n is a constant, typical for each parachute type, indicating the filling distance as a | ||
multiple of Do, dimensionless. | |||
The constant, n, will be called "fill constant" in subsequent discussions. The basic filling-time equation, | The constant, n, will be called "fill constant" in subsequent discussions. The basic | ||
filling-time equation, tf - n Do/v, has been extended by Knacke, Fredette, Ludtke, and others. | |||
The following formulations have provided good results. | |||
Ribbon Parachute | Ribbon Parachute | ||
tf- D•. | |||
where n - 8 (Knacke). | where n - 8 (Knacke). | ||
This equation gives accurate results with ribbon parachutes when the canopy porosities recommended in Chapter 6 are used. For small-diameter ribbon parachutes investigated in high-speed sled and rocket tests, Fredette found the following relationship: | This equation gives accurate results with ribbon parachutes when the canopy porosities | ||
recommended in Chapter 6 are used. For small-diameter ribbon parachutes investigated in | |||
high-speed sled and rocket tests, Fredette found the following relationship: | |||
tf=0. | tf = 0.65ATDo v | ||
where | where XT is the total canopy porosity expressed as a percent of the canopy surface area, So. | ||
Solid Flat Circular Parachute | Solid Flat Circular Parachute | ||
| Line 462: | Line 1,518: | ||
Wright Field investigations resulted in the following formulations: | Wright Field investigations resulted in the following formulations: | ||
nDo tf M= n-D V0.85 | nDo tf M= n-D V0.85 | ||
where n | where n - 4.0 for standard porosity canopig, and n = 2.5 fe. low porosity canopies. | ||
5-43 | 0 5-43 | ||
NWC TP 6575 | NWC TP 6575 | ||
Cross Parachute | Cross Parachute | ||
An investigator at NSWC, Silver Spring, Md., recommends | |||
. (CDS)pn | |||
where n - 8.7. The author has evaluated parachute fling-time data from free-flight tests and | |||
found that a formulation for filling time, where the line-stretch velocity, vs, is a linear function | |||
instead of an exponential function, gives satisfactory results in the medium-velocity range of | |||
about 150 to 500 ft/s. Table 5-6 lists the fill constant, n, in the equation tr -nD for a variety of v | |||
parachutes. | |||
TABLE 5-6. Canopy Fill Constant, n, for | |||
Various Parachute lypes. | |||
Canopy fill constant, n | |||
Paraxe type Res DWW Unreeofe | |||
opening opening opening | |||
Solid flat circular ID& ID a | |||
5 | Extended-skIrt, 10% 16-18 4-5 10 | ||
Extenled-skirt, full 16-18 7 12 | |||
Cross ID ID 11.7 | |||
Ribbon 10 a 14 | |||
Ringslot ID ID 14 | |||
Rlngsall 7-8 2 7 | |||
Ribless guide suudace ... ... 4-6 | |||
a ID = Insufficient data available for meaningful | |||
evaluation. | |||
Additional fill-factor data can be found in Table 6-1 of Reference 2.1. | |||
5- | The filling time of the various stages of reefed parachutes can be determined as follows: | ||
Do (CDS)R 1and t 5-4 - nD (CDS)o - (CDS)R 1/2 | |||
Vs (CDs), Vt (CDS)o | |||
5-44 | |||
NWC TP 6575 | NWC TP 6575 | ||
The | where | ||
tf, and tf2 are the reefed and disreefed filling times, | |||
vs and Vr are the velocities at line stretch and at disreef, ft/s | |||
(CdS)R and (CdS)o are the reefed- and full-open drag areas, ft2. | |||
Some solid textile, circular parachute types appear to have a critical opening velocity. At | |||
high velocities and high dynamic pressures, the canopy opens only partially. The drag of the | |||
partially opened parachute decelerates the parachute-vehicle system and the canopy opens | |||
fully. This type of opening can also occur on ribbon parachutes with porosities that are too | |||
high (Figure 6-23). Attempts to use this phenomenon for controlling the canopy inflation | |||
process, and thereby the parachute forces, have not been successful because of the variables | |||
involved and the difficulty of controlling the porosity of solid fabric canopies. | |||
Some types of ribbon parachutes have been opened in the velocity range of up to Mach | |||
4.0. Greene concludes that canopy filling time at supersonic speeds is constant, because the | |||
canopy operates behind a normal shock. Reference 5.82 presents test data that appear to | |||
confirm his investigations. | |||
In a NASA test program to develop parachutes for planetary landing, ringsail, cross, and | |||
disk-gap-band parachutes were opened successfully at altitudes above 100,000 feet and at | |||
speeds exceeding Mach 3.0. Section 5.5 provides further details on high-altitude effects, and | |||
section 5.8 describes supersonic parachute applications. | |||
5.4.4 Parachute Drag-Area Increase During Canopy Filling Process | |||
The parachute drag area, (CDS)p, increases from 0 to 100% during canopy inflation. The | |||
drag-area-versus-time increase--linear, convex, concave, or random-is well known and has | |||
proven to be constant and repeatable for known parachute types (see Figure 5-38). | |||
The drag-area-versus-time increase for reefed ribbon, ringsail, and extended-skirt | |||
parachutes is shown in Figure 5-39. | |||
RIBBON RINGSLOT CIRCULAR EXTENDED | |||
Figure 5-41 plots drag-area increase for the 63-foot-diameter reefed ringsail main parachutes used with the Mercury space capsule. It shows a typical characteristic of ringsail parachutes-the increase in drag area during the reefed stage. The ringsail parachute inflates rapidly into an initial reefed stage and then grows slowly through inflation of additional rings. This characteristic is advantageous for single parachutes because it constitutes a form of continuous disreefing, a highly desirable feature. | 1 7 | ||
l - , . k- t - tf1- t | |||
FIGURE 5-38. "lypical Drag-Area-Versus-Time Increase for Various Parachute ypos. | |||
5-45 | |||
NWC T? 6575 | |||
RIBBON EXTENDED RINGSAIL | |||
C./1/1 / | |||
,, I - I I.. . , | |||
FIGURE 5-39. lypical Drag-Arca-Verws-Time Increase for Reefed Parachutes. | |||
The shape of the drag-area-versus-time curve may be somewhat drawn out or | |||
compressed by reefing, changes in porosity distribution in the canopy, wide slots, or other | |||
means; however, the basic configuration of the curve is maintained for a particular type of | |||
parachute. | |||
Drag-area-versus-time curves are obtained from wind-tunnel or free-flight tests by | |||
dividing the measured instantaneous force by the instantaneous dynamic pressure. This, more | |||
precisely, should be called a dynamic drag area, because it includes characteristics that affect | |||
the opening process, such as apparent mass and altitude density. | |||
The evaluated drag-area-versus-time increase for unreefed, solid flat circular, ringslot, | |||
and personnel guide chutes (Figure 5-40), is taken from Reference 5.83. The author has added | |||
the typical drag-area increase for ribbon and extended-skirt parachutes, determined from | |||
numerous tests. Ribbon and ringslot parachutes have a strictly linear drag-area-versus�time increase, and solid textile parachute types have a rather uniform, concave form of | |||
drag-area increase. Ludtke found that this increase of solid textile parachutes could be | |||
expressed by | |||
(CDS)X r I | |||
(CIDS), Vf | |||
where q is the ratio of the projected mouth area of the canopy at line stretch to the projected | |||
frontal area of the fully opened canopy. | |||
Figure 5-41 plots drag-area increase for the 63-foot-diameter reefed ringsail main | |||
parachutes used with the Mercury space capsule. It shows a typical characteristic of ringsail | |||
parachutes-the increase in drag area during the reefed stage. The ringsail parachute inflates | |||
rapidly into an initial reefed stage and then grows slowly through inflation of additional rings. | |||
This characteristic is advantageous for single parachutes because it constitutes a form of | |||
continuous disreefing, a highly desirable feature. | |||
5-46 | 5-46 | ||
NWC | NWC 1? 6575 | ||
20 | |||
0 1 | |||
I S PERSONNEL GUIDE SURFACE | |||
o RINGSLOT CANOPY | |||
L ELLIPTICAL CANOPY | |||
1.6 0 SOLID FLAT CANOPY | |||
o 10% EXTENDED SKIRT | |||
1.4 V RIBBON | |||
o 1.2 | |||
0.." | |||
0/ | |||
Deo | |||
002 | |||
0. | |||
Ii | |||
0.GUR 5c40 DrgAe.atoVru/imninesFiln ie | |||
• ' / 0 | |||
g , / | |||
Data on drag-area-versus-time increase for the various parachute types are important for establishing the drag-area-versus-time diagrams required for the force-time-trajectory computer program described in this section and used in Chapter 7. | 0.4/ / / | ||
000 | |||
0 0.2 0.4 06 08 1 0 1.2 14 1 | |||
t, t | |||
S~FIGURE 5.40. Drag-Area Ratio Versus Dimensionless Filling Time. | |||
400- 2000 | |||
A = POINT OF MAXIMUM REEFED FORCE | |||
B - POINT OF MAXIMUM DISREEF FORCE | |||
300 N | |||
E, | |||
1 ISREEF, I SCALE . | |||
1400 2000 | |||
0 - | |||
A | |||
w | |||
300 10 2 | |||
,R 5 a o i 200 1000 | |||
uJIU | |||
0 O 20 30 40 50 60 70 80 9L | |||
TiME SECONDS | |||
FIGURE 5-41. Drag-Area-Venus-Time Diagram for the Mercury 64-Foot Ringsail Parac'hute. | |||
0 5.47 | |||
NWC TP 6575 | |||
Figure 5-41 also demonstrates the extremely short disreefing time of 0.8 second. | |||
References 5.50 and 5.79 include figures that show the drag-area increase for a single 85-foot�diameter Apollo ringsail main parachute. The increase in drag area during the reefed stage | |||
proved detrimental for the cluster of the three Apollo main parachutes because it tended to | |||
support nonuniform inflation. | |||
Reference 5.23 gives drag-area-versus-time data for reefed, extended-skirt parachutes. | |||
Several Sandia Reports (References 5.41 to 5.47) provide data on ribbon parachutes. | |||
Drag-area-versus-time increase for a 101-foot-diameter, triconical parachute is shown in | |||
Figure 5-42. The drag area in the reefed stage remains constant, which is typical for all known | |||
types of parachutes except the ringsail. As shown in Figure 5-40, the disreef drag-area curve | |||
displays the same concave shape as other solid textile parachutes. The triconical parachute, in | |||
contrast to the ringsail parachute (Figure 541), has a long disreef time (tf2 = 7.5 seconds), | |||
resulting in a relatively small canopy overshoot. | |||
Data on drag-area-versus-time increase for the various parachute types are important | |||
for establishing the drag-area-versus-time diagrams required for the force-time-trajectory | |||
computer program described in this section and used in Chapter 7. | |||
360 9000 | |||
F | |||
320- -P 8000 -F | |||
SREEFEDu 280 - 7000 -IREEF 1 wu 13 DISREEF cc | |||
S240 - 6000 , | |||
S200- 5000 o - | |||
Q 160- 4000 - .L_ | |||
wr U I "0120- ` 3000 - | |||
"LL so- 0 2000 | |||
40- 1000- tr SEC- - f2 | |||
O 0 I I _ | |||
0 2 4 6 8 10 12 14 16 18 20 22 24 | |||
TIME, SECONDS | |||
FIGURE 5-42. Drag-Area-Versus-Time Diagram for a Reefed | |||
101-Foot-Diameter Triconical Parachute. | |||
5-48 | 5-48 | ||
| Line 530: | Line 1,852: | ||
NWC TP 6575 | NWC TP 6575 | ||
Recovery system engineers should evaluate and publish drag-area-versus-time diagrams to improve the database for computing the force-trajectory-time analysis of parachute recovery systems. | Recovery system engineers should evaluate and publish drag-area-versus-time diagrams | ||
to improve the database for computing the force-trajectory-time analysis of parachute | |||
recovery systems. | |||
S.4.5 Effect of Canopy Loading, W/(CDS)p, on Parachute Opening Forces | |||
Figure 5-43 is a force-time diagram of a parachute opening in a wind tunnel. This pattern | |||
is typical for parachutes without velocity decay during parachute inflation and is called the | |||
"infinite mass" condition, because the parachute acts as if it were attached to an infinite mass. | |||
The | The same parachute dropped from an airplane and weighted for a 20 ft/s rate of descent | ||
parachute | will have the known force-time diagram of a personnel parachute (Figure 5-44). | ||
The personnel parachute dropped from an airplane has a finite load and is referred to as | |||
being tested, or used, under a "finite mass" condition. The primary difference between infinite | |||
and finite mass conditions is that, under infinite mass conditions, the velocity does not decay | |||
during parachute opening; whereas, under finite mass conditions, the velocity during | |||
• "-Fx /Fc | |||
F S Cx = Fx xl Fc | |||
FIGURE 5.43. Parachute Force Versus Time for a Wind-Tbnnel Test (Infinite Ma&.- Condition) | |||
/Fx | |||
FIGURE 5.44. Force Versus Time for a Personnel | |||
Parachute Drop (Finite Mass Condition) | |||
"-49 | |||
NWC TP 6575 | |||
parachute opening decreases substantially. Infinite and finite mass conditions can also be | |||
defined as conditions of high and low canopy loading, W/(CDS)p. | |||
An additional typical difference between infinite and finite mass conditions is the | |||
location of the peak opening force, F.. For a parachute opened under infinite mass conditions, | |||
or high canopy loading, peak opening force occurs at the first full canopy inflation. The peak | |||
opening force of a parachute opened at a finite mass condition will occur long before the | |||
parachute canopy is fully open. | |||
The relationship of the peak opening force, F., to the steady-state drag force, F., in | |||
wind-tunnel tests is defined as | |||
Opening-force coefficient, C, , = (see Figure 5-43). | |||
C, is a constant for a specific parachute type, as shown in Tables 5-1 through 5-5. | |||
With the newly defined opening-force coefficient, C,,, the equation for the parachute | |||
force can be written | |||
F, = (CDS)p q Cx X, | |||
where | |||
(CDS), = the drag area of the fully open parachute, ft2 | |||
q = the dynamic pressure at line (canopy) stretch, lb/ft2 | |||
C,- = the opening force coefficient at infinite mass, dimensionless | |||
X1 = opening-force-reduction factor, dimensionless. | |||
The force-reduction factor, X1, is 1.0 for a parachute opened at the infinite mass | |||
condition; close to 1 for high canopy loading drogue chutes (close to the infinite mass | |||
condition); and as low as 0.02 for final descent parachutes with a low canopy loading (finite | |||
mass). | |||
Table 5-7 shows the difference in opening forces and X1 factor for a 28-foot-diameter | |||
parachute opened at 180 KEAS behind an aircraft as a landing deceleration parachute; behind | |||
an ordnance device such as a bomb, mine, or torpedo for retardation; and as personnel | |||
parachute for an aviator. The difference in the force reduction factor X1 for the three | |||
applications is surprising. The primary reason for this effect is the difference in velocity decay | |||
during the parachute opening process. | |||
Figure 5-45 shows the force-time record of a 15.6-foot-diameter ringslot parachute | |||
opened behind a B-47 bomber at a 30,000-foot altitude. This parachute, used as an approach | |||
brake for descent from high altitude, has a canopy loading close to infinite mass condition, | |||
resulting in an X, factor of 1.0. | |||
5-50 | |||
NWC TP 6575 | |||
TABLE 5-7. Opening Forms and Canopy Loading of a 28-Foot-Diameter | |||
Parachute for Various Vehicle Applications. | |||
Vehicle Mass | |||
AppliCatkon welght, Ib (CoS)P, ftz W/(C0 S)P, llMft 2 Cx Fl, Ib X, condition | |||
Aircraft 140,000 490 286 1.7 91,200 1.0 Infinite | |||
Ordnance 2000 490 4.1 1.7 30.100 0.33 Intermedlate | |||
Petonnel 250 490 0.51 1.7 2900 0.032 Finite | |||
180 9000 AIRSPEED | |||
160 8000 x | |||
Fx =7,400 LB•._ | |||
140 - 7000 - | |||
u, 120 0 6000- F 6,800B | |||
5 z B-47 APPROACH PARACHUTE 100- 0 5000- | |||
0. TEST DATE: 5 MARCH 1954 | |||
I- . 15.6-FT-DIA RINGSLOT PARACHUTE | |||
Q 80 - 4000 - DEPLOYMENT ALTITUDE. 30.000 FT 0 Cr "J 0 AIRCRAFT WEIGHT 128.000 LB | |||
60- -- 3000 NCANOPY LOADING W (CD'S)o 2 1365 PSF | |||
I F. = 7,400 L8, F, - 6.800 LS | |||
40 - 2000 - F Cx .• 1 088, x I - 1.0 | |||
7-c | |||
20- 1000 tf -- CDo .49 | |||
0 0 oF_ __ __I _I _ l 1 2 3 4 5 6 7 | |||
TIME AFTER COMPARIA -.NT DOOR OPENING, SECONDS | |||
FIGURE 5-45. 15.6-Foot-Diameter Ringplot B-47 Approach Parachute Opening Forces. | |||
The clean, aerodynamic configuration of the B-47 bomber produced a shallow approach | |||
angle, making a point landing difficult. A 15.6-foot-diameter ringslot parachute was used | |||
instead of wing brakes or spoilers to increase the drag on approach and thereby steepen the | |||
glide angle. At touchdown, a 32-foot-diameter ribbon parachute was deployed as a | |||
deceleration parachute side-by-side with the ringslot parachute. Deploying the parachutes at | |||
even skirt levels assured successful opening of the second parachute. Note that the aircraft | |||
velocity does not decay during parachute inflation. | |||
Figure 5-46 shows the opening process and the opening force versus time for a | |||
29-foot-diameter, guide surface personnel parachute tested at 250 knots at the El Centro, | |||
Calif., whirl tower. The difference in the force-versus-time diagram, with the ringslot | |||
0 5-51 | |||
NWC TP 6575 | |||
LEGEND | |||
A = DROP | |||
8 z CANOPY LINE STRETCH. F, | |||
C = MAXIMUM PARACHUTE FORCE. F 3.740 LB | |||
D CANOPY HALF INFLATED | |||
E = FIRST FULL CANOPY INFLATION | |||
4,000 | |||
C | |||
3.000 | |||
2.,2000 | |||
0 | |||
UIf | |||
0.1 0.2 0.3 04 05 06 0.7 08 09 10 TIME. 11 SEC1.2 1.3 1.4 15 16 17 18 1.9 20 21 22 | |||
FIGURE 5-46. Opening Proess and Opening Forme Venus Time for a Guide Surface Personnel Parachute | |||
Tested at the El Centro Whirl Tower at 250 Knots With a 200-Pound Torso Dummy. | |||
parachute opened behind the B.47 aircraft, is obvious. The maximum opening force, F1, | |||
occurs when the parachute canopy has reached about one-third of its inflated diameter. The | |||
force at full open canopy has decreased to about 600 pounds, indicating that parachute | |||
velocity during opening has decreased almost to equilibrium velocity. The velocity decay | |||
during opening results in an opening-force-reduction factor, X1. of 0.0239. | |||
Another important characteristic is the relative size of the snatch force. On high canopy | |||
loading parachutes, where the parachute mass is small compared to the mass of the vehicle to | |||
be decelerated, the snatch force is small if the deployment system is good, as described in | |||
Chapter 6. On low canopy loading parachutes, where the mass of the parachute can be 3 to 7% | |||
of the mass to be decelerated, the snatch force can reach or surpass the maximum opening | |||
force unless a proper deployment method is used. | |||
All parachute applications fall into distinctive groups of canopy loading, W/(CDS)p. | |||
Canopy loading is equivalent to dynamic pressure at equilibrium velocity and therefore relates | |||
to rate of descent. Figure 5-47 shows this relationship. | |||
5-52 0 | |||
NWC TP 6575 | |||
10009" | |||
500 | |||
400 | |||
S300 | |||
200 | |||
LU 100 200 500 1000 1500 | |||
L" 100 (•I PERSONNEL & CARGO | |||
LL PARACHUTES | |||
U MISSILE MAIN RECOVERY | |||
L, ;l PARACHUTES | |||
U- 5 | |||
•: 4 •,•.• rM ORDNANCE PARACHUTES 40 | |||
er17 SUBSONIC MISSILE DROGUE | |||
3• CHUTES | |||
A Y A G S V LANDING DECELERATION 13 PARACHUTES | |||
20 MZ SUPERSONIC MISSILE | |||
DROGUE CHUTES | |||
I LANDING APPROACH | |||
•/ PARACHUTES | |||
0.1 0.5 1.0 5.0 10 50 100 | |||
•. CANOPY LOADING W/CDS)p, PSF | |||
FIGURE 5-47. Rate of Descent Versus Canopy Loading and Parachute Applications. | |||
The seven application groups in Figure 5-47 can be combined into three groups in | |||
relation to the force-reduction factor, X1. Groups I and II will have X1 factors in the 0.02- to | |||
0.25-range (personnel and cargo) parachutes. Group III (ordnance) parachutes have X1 | |||
factors in the 0.3 to 0.7 range. These parachute groups operate at finite mass conditions. All | |||
parachutes in Groups IV to VII have X1 factors close to or equal to 1.0 and operate at infinite | |||
mass conditions. | |||
5.4.6 Methods for Calculating Parachute Opening Forces | |||
Three methods for calculating parachute opening forces are discussed in this section. | |||
Method I, the W/(CDS)p method, is fast but should be used for preliminary calculations only. | |||
Method 2, the Pflanz method, is mathematically exact and provides good results within certain | |||
application limits. Method 3, the previously mentioned computerized force-trajectory-time | |||
method, gives good results with no limitations. However, all three methods require knowledge | |||
of certain parachute and opening-process characteristics. | |||
0 5-53 | |||
NWC TP 6575 | |||
Method 1, W/(CDS)p Method. The equation for the parachute opening force, FX, was | |||
defined in section 5.4.5 as | |||
F. - (CDS)p q Cx X I | |||
where | |||
(CDS)p - the drag area of the full open or reefed parachute, ft2 | |||
q - the dynamic pressure at line stretch or disreef, Ib/ft2 | |||
C- - the opening-force coefficient at infinite mass, dimensionless (TIbles 5-1 | |||
through 5-5). Do not use C. at low canopy loading | |||
X, - the force-reduction factor (the unknown factor in this equation), dimensionless | |||
For an unreefed parachute, the drag area, (CDS)p1 of the full open parachute is used. For | |||
a reefed parachute, a preliminary reefed drag area, (CDS),, can be calculated from the | |||
allowable maximum parachute force, F1, and the dynamic pressure at line stretch: | |||
(CDS)R = F | |||
qC3 Xi | |||
For this preliminary calculation, an opening-force coefflicient, C1, of 1.0 should be used | |||
for the reefed parachute. The force-reduction factor, X1, can be estimated as 1.0 for reefed | |||
drogue chutes and 0.9 for reefed main parachutes. | |||
For the actual force calculations for unreefed parachutes, the force coefficient in | |||
Tables 5-1 through 5-5 applies. Reefed parachutes have different opening-force coefficient | |||
factors for the reefed and disreefed stages. Figures 5-41 and 5-42 show the drag-area-versus�time diagrams for a reefed ringsail and a reefed triconical parachute. There is no drag | |||
overshoot for both parachutes when they open in the reefed stage. Therefore, the opening�force coefficient is 1.0. If evaluations from previous tests are not available, a C, coefficient of | |||
1.1 should be used. For the disreef stage, the force coefficient evaluated from test data should | |||
be used, if available; otherwise, Tables 5-1 through 5-5 will provide acceptable data. | |||
For obtaining the opening-force reduction factor, XI, the canopy loading of the full open | |||
or the individual reefed stages is calculated and the appropriate X1 factor as a function of | |||
canopy loading is found in Figure 5-48. | |||
The amount of parachute force fluctuation in the wake of the forebody must be | |||
considered when calculating the opening force of a small drogue chute behind a large | |||
forebody. This fluctuation is illustrated in Figure 5-49, which shows the effect of the Apollo | |||
space capsule's wake on the opening force of the 16.5-foot-diameter ribbon drogue chute | |||
(Reference 5.10). | |||
5-54 | |||
NWC TP 6575 | |||
1.0o00 | |||
x 0 .8 | |||
0 | |||
. / | |||
Ur- 0.4 /001 | |||
LU | |||
L Dc 0.2 - - F x = (C b) S i) • • • X 1 | |||
0 | |||
o | |||
U. | |||
0.1 | |||
0.0 | |||
0.2 0.4 0.6 0.8 1.0 2.0 4.0 6.0 8.0 10 20 40 60 80 100 | |||
PARACHUTE CANOPY LOADING, (W/(CD S)p. PSF | |||
FIGURE 5-48. Opening-Force Reduction Factor Versus Canopy Loading. | |||
FORCE-TIME VEHICLE VEH:;LE | |||
TRACE CONFIGUR - DESIGNATION DIAMETER ATION FT | |||
BOILERPLATE 11 | |||
SJ COMMAND | |||
MODULE | |||
4(IP CM) | |||
TIME | |||
PARACHUTE $a | |||
TEST VEHICLE | |||
U IPTV ) | |||
TIME | |||
INSTRUMENTED 30 CYLINDRICAL | |||
TEST VEHICLE ( ICTV) | |||
ex 1 09 | |||
TIME | |||
FIGURE 5-49. Apollo Ribbon Drogue Chute | |||
Force Fluctuation Caused by ForebodyWake | |||
(Inflated Parachute Diameter, Dp. is 10.7 feet) | |||
5-55 | |||
NWC TP 6575 | |||
The increase in load fluctuation from the small ICTV to the large-diameter boilerplate 0 | |||
command module (B/P CM) is apparent in the increase of the force coefficient, C1 , from 1.09 to | |||
1.31. The force coefficient in Figure 5-49 is actually the product C, times X1, called Ck. | |||
However, at the canopy loading of the drogue chute, X1 will be close to 1.0, approaching the | |||
infinite mass condition. | |||
The X1 factor can be obtained from drop tests by calculating | |||
(CDS) q | |||
and then plotting it versus W/(CDS)p. The data in Figure 5-48 were obtained by this method. | |||
The X 1 factor in Figure 5-48 does not include the effect of altitude. Opening forces of | |||
high-canopy-loading parachutes change little with altitude. However, the effect of altitude on | |||
low-canopy-loading parachutes, such as personnel parachutes, is considerable. For | |||
low-canopy-loading parachutes, the X, factors should be used only for altitudes below 15,000 | |||
feet. Section 5.5 contains a discussion of the altitude effect on parachute forces. | |||
Ewing evaluated and plotted the Ck = C,,Xt factor from numerous tests of ringsail | |||
parachutes (Reference 5.50). | |||
French recommends plotting a Ck = C,,X 1 factor versus a mass parameter in the form | |||
Do3/m, where Do is the nominal diameter of the parachute and m is the mass of the vehicle and | |||
the parachute assembly (Reference 5.80). | |||
Schilling recommends modifying this mass parameter to the form | |||
Rm = P(CDS)p | |||
3/ 2 | |||
mt | |||
where mt is the total mass of vehicle plus decelerator, p is the air density, and (CDS)p is the | |||
parachute drag area (Reference 5.81). The value p. (CDS)p3/ 2 represents the volume of the air | |||
in and around the parachute canopy and has an obvious relationship to the apparent mass. | |||
The | The altitude effect is now included in plotting Ck factors versus this mass parameter, Rm. | ||
Figure 5-50, taken from a Northrop publication, shows Ck factors for reefed and unreefed | |||
ribbon and ringslot parachutes plotted versus the mass parameter. These data include | |||
supersonic deployment of ribbon parachutes. | |||
Method 2, Pflanz Method. The Pflanz method was developed in Germany during World | |||
War II by E. Pflanz in cooperation with the author. It was based on the following concept. A | |||
body of known fixed weight and velocity is decelerated along a horizontal flight path by an | |||
aerodynamic drag device whose drag area increases from a small value to 100% in a known, | |||
mathematically definable form. This method is mathematically exact; however, no (CDS)p | |||
overshoot is included at the start of the reefed or disreefed inflation cycle. Details of this | |||
method may be found in References 5.76 and 5.77. | |||
5-56 0 | |||
NWC TP 6575 | |||
16-2 | |||
Ne 1.2 AA 15212 | |||
U1.2 1.29 -0 a. | |||
ol i I , _ | |||
II o I I i _ | |||
o w 1.34 P 2 | |||
0-1.34 .- 1.56 | |||
K3/2CS MASRTOZM C ~ | |||
LU0.80 | |||
0 | |||
MAS -KIO RM~s = C 1 | |||
Mt | |||
S~PARACHUTE DATA | |||
SYMBOL FOREBODY | |||
TYPE DoFT M REEFING RATIO METHOD DEPLOY | |||
SAPOLLO CONICAL RIBBON DROGUE 137 0308 MORTAR BUFF | |||
SAPOLLO CONICAL RIBBON DROGUE 165 0.428 MORTAR BUFF | |||
0 ADDPEP HEMISFLO 16.0 0.22-041 CANISTER STREAMLINED | |||
SMERCURY CONICAL RIBBON 6.87 0.87 MORTAR STREAMLINED | |||
SSANDIA CONICAL RIBBON 20.0 0.186 DROGUE GUN STREAMLINED | |||
C COOK CONICAL RIBBON 844 0.20-030 PILOT CHUTE STREAMLINED | |||
o UAR RINGSAIL 20-30 0.16-0.31 PILOT CHUTE STREAMLINED | |||
E3 CENTURY RINGSAIL 128 0.125 PILOT CHUTE STREAMLINED | |||
SASSET RINGSAIL 29.6 0.10'0.20 P'LOT CHUTE STREAMLINED | |||
5. | APOLLO BLK 1HEAVY RINGSAIL 83.5 0.08 F LOT CHUTE STREAMLINED | ||
t APOLLO BLK I AND 7r RINGSAIL 835 0.095 PILOT CHUTE STREAMLINED | |||
FILLED SYMBOLS INDICATE SUPERSONIC PARACHUTE DEPLOYMENT. NUMBERS ADJACENr TO DATUM | |||
POINTS IDENTIFY MACH NO. AT PARACHUTE LINE STRETCH | |||
FIGURE 5-50. Opening-Force Factor Versus Mass Ratio. | |||
5-57 | |||
NWC TP 6575 | |||
A dimensionless ballistic parameter, A, is formed from known or calculated data | |||
A=- 2Wt | |||
(CDS)ppgVltf | |||
where | |||
A - ballistic parameter, dimensionless | |||
Wt = system weight, lb | |||
(CDS)p - parachute drag area, reefed or fully open, ft2 | |||
g = acceleration of gravity, ft/s 2 | |||
v, - velocity at line stretch or start of disreef, ft/s | |||
p = air density at altitude of parachute inflation, slugs/ft3 | |||
tf = canopy inflation time | |||
Wt, q. p are fixed values for each specific application, as is the drag area of the fully open | |||
parachute, (CDS)p. A preliminary drag area of the reefed parachute, (CDS)r, can be calculated | |||
as described in Method 1. The reefed filling time, tf,, and the canopy disreefing time, tf2, are | |||
5. | calculated by the method given in section 5.4.3. After calculating the ballistic parameter, A, the | ||
force-reduction factor, X1, is obtained from Figure 5-51. However, before determining X1, the | |||
shape of the drag area increases versus time must be determined for the selected parachute. | |||
This | This drag-area-versus-time rise is denoted in Figure 5-51 by the letter n. The n = I curve is a | ||
straight line, typical for ribbon and ringslot parachutes. The concave curve, n = 2 is | |||
representative of solid cloth, flat circular, conical, extended-skirt, and triconical parachutes | |||
described in section 5.4.4. The convex form of (CDS)p versus time occurs only in the reefed | |||
inflation of extended-skirt parachutes. Refer to the comments on the C,, factor of Method I for | |||
low-canopy-Icading, unreefej parachutes. | |||
The Pflanz report provides extensive information on forces, time of maximum force, and | |||
5. | velocity decay versus time during the parachute inflation process for a variety of drag-area�versus-time increases other than those shown in Figure 5-51. | ||
After the force factor, X1, is determined from Figure 5-51, the opening force of the | |||
parachute is calculated as it was in Method I | |||
Fp- (CDS)p ql(Cx)X1, lb | |||
5-58 | |||
NWC TP 6575 | |||
1.0 | |||
0.9 n2 ..- - 1 __ _ | |||
0.8 CURVES II 0.7 _ _ _ _ | |||
X 0.5 n 1/2n 1/2 | |||
n !-' r1 ' | |||
c 0.4 -- I--1"- CD S)p n -. | |||
0.39 ,, "" 0 | |||
0. | |||
0O.0~~7 ,, - __ / __ | |||
• 0.06 2 | |||
0.1 | |||
Cc 0.04 n-- ~p •P "g• 1•t | |||
0.07 F = (CD ' S~O ci C• X1 W0.05 | |||
o o 2 0 A ocO�CURVE I | |||
SII I I1 I I 1 1 1 1 I I I I I I1 1 I I I1 1 1I I I I | |||
I- , | |||
CURVE I | |||
BALLISTIC PARAMETER, A | |||
FIGURE 5-51. Opening-Forcc Reduction Factor, X1, Vcrsus Ballstic Parameter, A. | |||
where | |||
(CDS)p - the drag area of the fully open or reefed parachute | |||
qj - the dynamic pressure at the start of inflation or at disreef | |||
C, = the opening-force coefficient for the reefed or unreefed parachute. To be used | |||
only for high canopy loading conditions | |||
5 | X1 = the force-reduction factor determined from Figure 5-51 | ||
Frequently, a velocity decay occurs between vehicle launch and canopy (line) stretch, V1. | |||
This decay can be calculated for deceleration in a horizontal plane | |||
V1 Vo | |||
1+ r [ ic~s) p --g t, v.] 59 | |||
S~5-59 | |||
NWC TP 6575 | |||
where | |||
Vo - velocity at the beginning of deceleration. All other notations are similaLr to those | |||
previously used | |||
5. | The second Pflanz report (Reference 5.77) expands on the first report by determining | ||
parachute forces and velocity versus time for straight-line trajectories of 30,60, and 90 degrees. | |||
Ludtke, in References 5.83 and 5.84, has somewhat generalized the Pflanz method and | |||
has included determination of parachute opening forces from deployment of any trajectory | |||
angle. | |||
Method 3, Force-Trajectory-Time Method. The force-trajectory-time method is a | |||
computer approach to the parachute opening process. The recovery-system specification for | |||
an air vehicle, drone, missile, or aircrew escape system normally defines the starting and | |||
ending conditions of the recovery cycle, including weight of the vehicle, starting altitude. | |||
velocity, vehicle attitude; and for final recovery or landing, the specification defines the rate of | |||
descent at landing and the oscillation limitation. The maximum allowable parachute force is | |||
frequently expressed in g as a multiple of the vehicle weight. A typical requirement limits the | |||
parachute opening force to 3 to 5g, necessitating a multiple-stage recovery system consistingof | |||
a reefed drogue chute and one or more reefed main parachutes. | |||
These conditions require optimization of the total recovery cycle for minimum recovery | |||
time, altitude, and range within the allowable parachute force restraints. The computer, with | |||
its multiple-run capability that permits many variations in staging, timing, and altitude, is the | |||
ideal tool to accomplish this task. | |||
A force-trajectory program best meets the above requirements for calculating the vehicle | |||
trajectory and deceleration as well as parachute forces as a function of time. The basic | |||
approach is somewhat similar to the Pflanz method. A drag-area-versus-time profile is formed | |||
for the total system vehicle plus decelerator. Multiple computer runs are made using the | |||
Revision as of 15:19, 17 June 2024
PARACHUTE CHARACTERISTICS AND PERFORMANCE
Parachutes are the building blocks of any parachute recovery system. Their performance characteristics must be known and considered in selecting and designing a system. In the early 1920s, the circular, flat parachute manufactured from solid cloth was the primary parachute used for the rescue of aviators, for sport jumping, and for airdrop of light loads. In the 1930s, the military began using parachutes for the airdrop of troops and cargo and for the landing deceleration of aircraft. Beginning in the 1940s, parachutes were used for recovery of unmanned aircraft, missiles, ordnance devices, and, later, recovery of manned and unmanned spacecraft.
These new parachute applications resulted in, or were the result of, the development of numerous new types of parachutes. The new parachutes were superior to the circular, flat, solid textile parachutes in stability, opening forces, and drag. Some of the new types could be used for supersonic applications and others for descent in a gliding mode. However, the superior performance characteristics were not combined in one parachute. Prudent analysis, therefore, is a requisite for matching the appropriate parachute to the desired application.
5.1 PARACHUTE DECELERATOR TYPES
Common parachute types, varying in stability, drag, opening behavior, velocity capability, and other design and performance characteristics, are listed in Tables 5-1 through 5-5, which are updated from the tables in Reference 2.1. The performance data are to be used for preliminary considerations only. Detailed performance data are found in sections 5.2 through 5.10 and in the references (section 5.12). The following comments refer to the column headings in Tables 5-1 through 5-5.
Constructed Shape. The Plan and Profile columns define the constructed diameter and the cross section of the parachute canopy.
, the constructed diameter of the canopy, can be obtained from the drawing of the specific parachute.
Nominal Diameter. Do, the nominal diameter of the parachute, can be calculated from the total canopy surface area, So, including the area of the vent and all other openings:
Inflated Shape. , the projected diameter of the inflated parachute canopy, is best calculated from the projected or inflated canopy area, , as measured in wind-tunnel tests. The projected diameter of a parachute varies with parachute type, canopy porosity, suspension-line length, velocity, and canopy design. A large projected diameter, , will generally result in a large drag coefficient, . The ratio of projected diameter to nominal diameter, , is an indication of the drag effectiveness of the parachute design, the larger the projected diameter in relation to the nominal diameter, the larger the drag coefficient.
Drag Coefficient. is the drag coefficient related to the total canopy surface area, . The drag coefficient indicates how effectively a parachute canopy produces drag with a minimum of cloth area, thereby minimizing weight and volume.
Opening-Force Coefficient. , the opening-force coefficient, indicates the difference between the instantaneous opening force and the steady drag force at constant speed. This condition, called the infinite mass case, is obtained in wind-tunnel tests and in parachute applications with high canopy loadings, , as exemplified by aircraft deceleration parachutes and first-stage drogue chutes.
Average Angle of Oscillation. The angle of oscillation is measured in wind-tunnel tests or during free-flight tests. Oscillation on most solid textile parachutes varies with size and descent velocity. Large parachutes oscillate less than small parachutes. Unstable parachutes tend to descend in an oscillating mode at rates of descent in excess of 25 ft/s, glide at descent rates below 15 ft/s, and mix glide and oscillation during medium rates of descent.
General Application. The general application column in Tables 5-1 through 5-5 indicates the primary use of the particular parachute type.
, in Table 5-4 is the wetted upper canopy surface area on gliding parachutes.
in Table 5-4 is the ratio of the upper surface area to total cloth area, including all ribs and stabilizer panels.
Referenced reports for most of the listed parachutes will be found in subsequent sections of Chapter 5, but primarily in section 5.2, Parachute Drag and Wake Effects.
Figures 5-1 through 5-15 show some of the more common parachute-type decelerators listed in Tables 5-1 through 5-5.
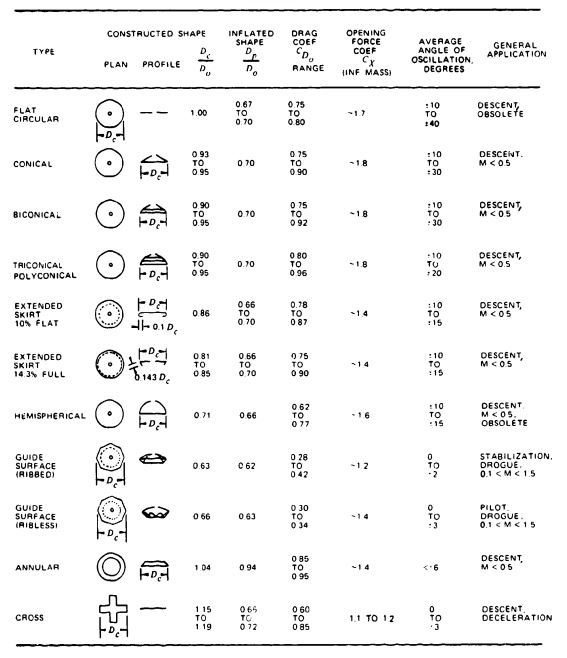
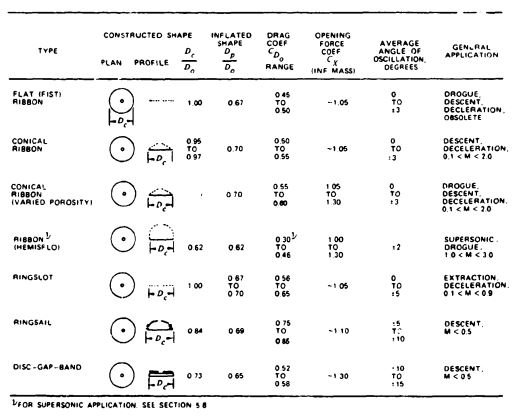
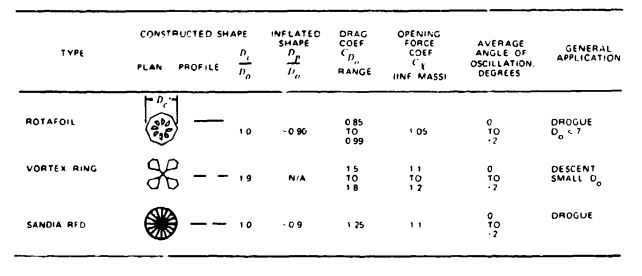
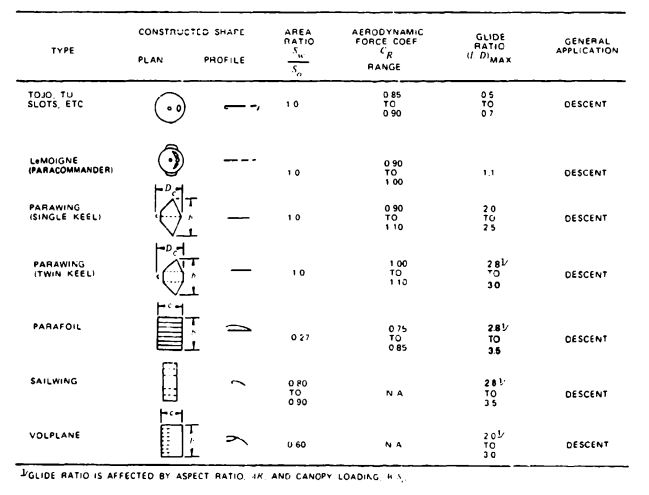
Note: Maneuverable parachutes with a glide ratio L/D of 2.5 or better have been defined in the literature as "hi-glide parachutes." This includes the parawing, the parafoil, the sailwing, and the volplane.
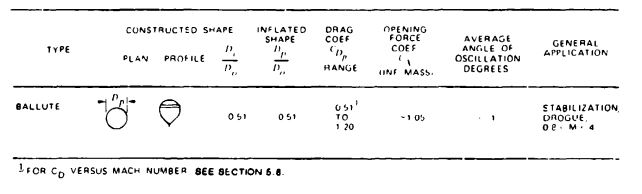











5.2 PARACHUTE DRAG AND WAKE EFFECTS
Parachute drag is an important performance parameter. because it determines the rate of descent, generally a primary performance consideration in the design of a parachute system. To maintain a required constant rate of descent, the drag of the parachute must equal the weight of the total system, as discussed in Chapter 4. The parachute drag, D, is
where
is the parachute drag coefficient related to the canopy surface area, dimensionless
is the canopy surface area, including the vent area and all openings and slots in the canopy,
is the dynamic pressure, equal to
For a given rate of descent, the dynamic pressure, q, is a fixed value. The product, , * is called the drag area of the parachute and is measured in square feet. A large drag coefficient, ,will result in a small canopy surface area, , and a low parachute weight and volume. Because these characteristics are highly desirable for large-diameter, final descent parachutes, a large drag coefficient is frequently the deciding factor in the selection of a parachute. The following design features and parachute canopy characteristics are known to produce high drag coefficients:
1. Conical, multi conical, or quarter-spherical canopy shapes
2. Rectangular or triangular canopy shapes
3. Long suspension lines
4. Low canopy porosity
5. Annular canopy shapes
6. Rotating parachutes
7. Gliding parachutes
The drag coefficient, , refers to the vertical component of the parachute velocity, as discussed in Chapter 4.
The glide velocity of a gliding parachute changes little with glide angle. However, the vertical component of the glide velocity (the rate of descent) decreases notably with an increasing glide ratio.
Rectangular and triangular parachutes up to personnel-parachute size have been used successfully at lower speeds. Deployment of large rectangular and triangular parachutes has caused problems. The noncircular canopy design makes it difficult to maintain tension on all canopy elements during deployment and inflation.
Long suspension lines increase the inflated diameter of the canopy and result in a larger drag coefficient, which, for a given rate of descent, produces a smaller diameter and a lighter parachute assembly.
Rotating parachutes have been used successfully with diameters up to 10 feet. Attempts to use larger rotating parachutes have resulted in poor deployment and canopy wrap-up before full inflation. Inaccuracies in the angle of pitch of individual gores cause variations in parachute rotation and drag coefficient.
Decreasing the porosity increases the drag coefficient but also produces a less stable parachute and a higher opening force.
Canopy profiles of quarter-spherical shapes and the similar tri conical shapes have shown the highest drag coefficients for circular canopy designs. * In this manual, , and are interchangeable.
5.2.1 Canopy Shape and Suspension Line Length Effects
In 1949, the U.S. Air Force conducted model drop tests of 1600-square-inch parachutes under controlled conditions in the Lakehurst, New Jersey, airship hangar (Reference 5.1). These tests established several facts previously unknown or only suspected.
Solid textile parachutes of a round or cornered design and with a flat or shaped profile descended in a vertical line, but oscillated violently when dropped at rates of descent greater than 30 ft/s. The same parachutes, when dropped with a low weight, had a 10-ft/s rate of descent and descended in a stable, non oscillating attitude, but glided at angles up to 45 degrees. In the 15-to 25-ft/s descent range, these parachutes combined oscillation with straight descent, or with glide but no oscillation. Gliding resulted in a low vertical velocity component and a high drag coefficient. Vertical descent with oscillation at the higher rates of descent resulted in lower vertical drag coefficients.
For the same surface areas, conical and quarter-spherical canopies had higher drag coefficients than circular flat canopies. Figure 5-16 shows that, at a rate of descent of 20 ft/s, a 30-degree conical parachute has a 9.5% higher drag coefficient than a flat, circular canopy, and a quarter-spherical canopy has a 14.5% higher drag coefficient. These tests were the basis for the quarter-spherical profiles of the ringsail and the triconical parachute canopies.
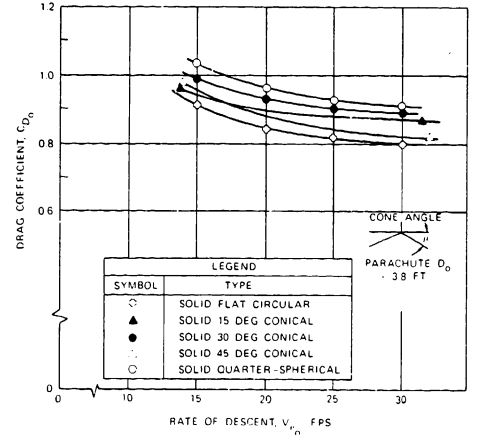
The model test results were confirmed in full-scale drop tests conducted at El Centro, Calif., with modified 28-foot-diameter personnel parachutes. Successive gores were removed from a 28-foot-diameter, flat, circular canopy to convert it into a conical parachute of increasing cone angles. The vertical drag coefficient, , increased with increasing cone angle and decreasing rates of descent. A cone angle of 25 to 30 degrees was the optimum angle, as shown in Figure 5-17 and Reference 5.2.
Data from Reference 5.1 (Figure 5-18) demonstrate the difference in drag coefficient, , versus rate of descent for four parachute types. Two types are stable: a flat, circular, ribbon parachute and a guide surface parachute. Two types are unstable: a solid textile, circular, flat parachute and a solid textile, square, flat parachute. Figure 5-18 clearly shows the characteristic that unstable parachutes increase their drag coefficient with decreasing rates of descent because of the change in descent behavior from oscillation to glide.
An increase in drag coefficient for a specific parachute can be accomplished by increasing the length of the suspension lines (see Figure 5-19). The increase in suspension-line length causes the parachute to open wider with a larger inflated area, , and inflated diameter, . The drag coefficient, related to the inflated (projected) area, , decreases slightly with an increase in line length and a related increase in projected diameter (see Figure 5-19b). However, the drag coefficient clearly increases with an increase in suspension-line ratio, (Figure 5-19a).
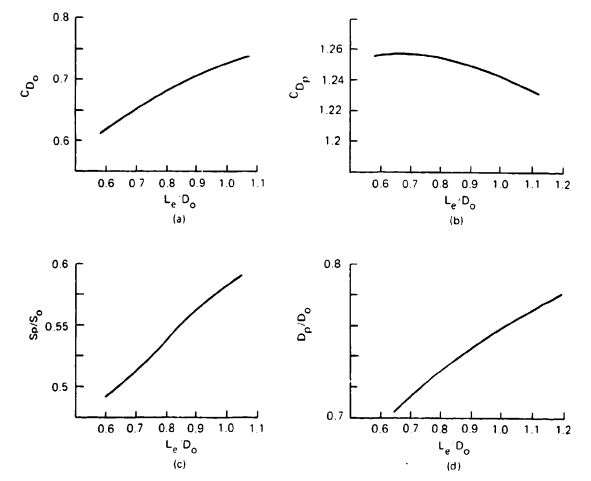
. The drag coefficient, , related to the inflated (projected) area, , decreases slightly with an increase in line length and a related increase in projected diameter (see Figure 5-19b). However, the drag coefficient clearly increases with an increase in suspension-line ratio, (Figure 5-19a).
The slopes of the curves for area and projected diameter growth in Figure 5-19 indicate that using suspension-line ratios larger than 1.1 may have provided additional drag.
These data were obtained in model tests with 1-meter (3.3-foot)-diameter parachutes. Reference 5.3 provides background on the tests. Figure 5-20 shows the possible increase in drag coefficient for line ratios, , up to 2.0. Parachutes with no skirt restrictions, such as flat and conical circular parachutes, increase the drag coefficient up to line ratios of 2.0. Parachutes with skirt restrictions, such as extended skirts and hemispherical canopies, show little drag coefficient increase at line ratios above 1.1. The data in Figure 5-20, taken from United States, British, and German sources, show relatively good concordance.
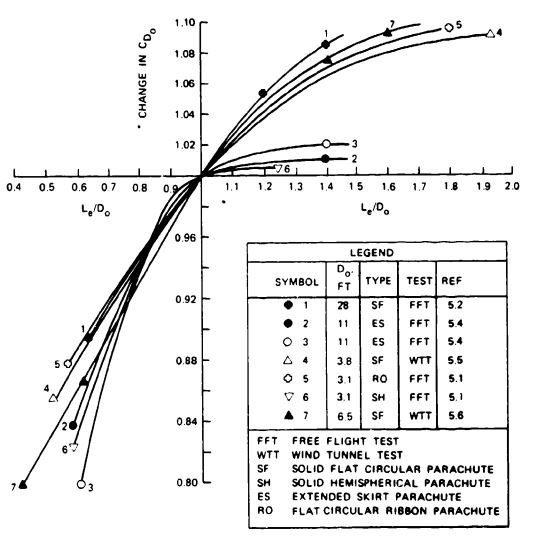
Calculations indicate that line-length ratios above 1.5 may be detrimental because of the associated weight increase of the longer lines. Systems that employ parachutes in clusters or use first-stage drogue chutes require long risers. Parts of these risers may be replaced by longer suspension lines on the individual parachutes to increase parachute drag and decrease the required parachute diameter and parachute assembly weight.
5.2.2 Forebody Wake Effect
Parachutes are always used in connection with a forebody, such as a parachute jumper, an aircraft, a load platform, or an Apollo-type space capsule. Each forebody produces a wake
that affects the parachute, depending on the relationship of the inflated parachute diameter,
DP, to forebody diameter, DB, and the distance between the end of the forebody and the
leading edge of the inflated parachute canopy. Figure 5-21 illustrates the drag loss. A cargo
container descending on a 100-foot-diameter parachute produces little wake effect, because
both the diameter ratio, Dp/DB, and the distance between the container and the leading edge of
the parachute, LT, are large. The inflated diameter of the Apollo drogue chute was smaller
than the diameter of the Apollo spacecraft. The distance between the leading edge of the
parachute and the rear of the spacecraft was kept to a minimum to save weight. Many
parachute jumpers have experienced the failure of a spring-loaded pilot chute that was ejected,
but then collapsed and fell back on the jumper because of the blanketing or wake effect of the
jumper's body. 0 Tests conducted in the NASA and Wright Field vertical wind tunnels determined that for
vertical descending bodies, the parachute should be ejected to a distance equivalent to more
than four times-and preferably six times-the forebody diameter, into good airflow behind
the forebody. Applying the six-forebody-diameter rule has been successful on Apollo and
other programs. Ejecting the parachute from a horizontal attitude or sideways out of the
forebody wake can provide good inflation with shorter forebody-to-parachute canopy
distances. However, successful inflation with shorter distances should be proven in tests of the
most unfavorable-not the most favorable--deployment conditions.
Deploying a small parachute in the wake of a large forebody also causes considerable loss
in parachute drag and may affect the stability of the parachute. Drag losses of up to 25% have
been experienced in wind-tunnel and free-flight tests. Figure 5-21 presents parachute drag
losses caused by forebody wake measured in wind-tunnel and free-flight tests. The two dotted
lines (I in Figure 5-21) encompass parachute wake loss data measured in wind-tunnel tests by
the University of Minnesota and the California Institute of Technology (Cal Tech) (References
5.7 through 5.9). Superimposed on this wind-tunnel data are free-flight test results obtained on
the reefed 16.5-foot-diameter Apollo command module drogue chute tested behind three
different forebodies. This drogue chute was tested behind (1) an 11.9-foot, boilerplate
command module (CM) (II in Figure 5-21), (2) a 5.8-foot-diameter parachute test vehicle
(PTV) (III), and (3) a 36-inch-diameter instrumented cylindrical test vehicle (ICTV) (IV)
0 5-21
NWC TP 6575
Op 1.0 "3""
0.9
LEGEND
0.B FOREBODY CANOPY
0.7
I-. 01 1.0 D8__ __ _ __ __ _ __ __ _
Z B0 I DATA FROM REFERENCES 5.3 TO 5.11
M 0.6 13 APOLLO DROGUE CHUTE BEHIND CM" =
w In APOLLO DROGUE CHUTE BEHIND PTV"' =
0 I APOLLO DROGUE CHUTE BEHIND ICTVIJ =
I XS-2 DROGUE CHUTE, REF 5.11 =
c 0 E SANDIA WIND TUNNEL TEST. REF 5.12 A £
ICD = PARACHUTE DRAG COEFFICIENT
CD,,= DRAG COEFFICIENT WITH NO FOREBODY
0.4I
0 NEGATIVE \ BASE PRESSURE REGION
2 4 6 8 10 12 14 15 16 18 20
RATIO, LT/DB
_i SEE FIGURE 5-22 FOR DEFINITIONS.
FIGURE 5-21. Parachute Drag Loss Caused by Forebody Wake.
5-22 O
NWC TP 6575
(Reference 5.10). These measured Apollo parachute data agree well with data from the
University of Minnesota and the Cal Tech wind-tunnel tests.
Parachute wake effect data measured in wind-tunnel tests behind a 3/8 scale model of the
ejectable nose section of the XS-2 research aircraft (V)(Reference 5.11), and data measured on
model parachutes by the Sandia National Laboratories (VI) (Reference 5.12), are included in
Figure 5-21.
Figure 5-22 details the measured forebody wake effect on the 16.5-foot-diameter ribbon
drogue chute of the Apollo Command Module shown in Figure 5-21.
Many forebodies, such as aircraft, have a noncylindrical cross section. Figure 5-23
demonstrates a method that has been used successfully to convert an odd-shaped cross section
to a circular area. The area of the forebody, SB, included in the inflated area of the parachute
behind the forebody is converted into the area of an equivalent circle. The diameter of this
circle, DB, is then used as the reference forebody diameter.
f
140 I1.0 (C S)p
0 1.0 1 _o
DRAG 0 0.92 01 0 (CD S).
AREA 120 - 01 0TCDs 0 0.82 08
100- 0
FOREBODY I
DIAMETER 11.9 5.8 3.0
(FT)-
CONFIGURATION __
DESIGNATION 8/P CM PTV ICTV
VHCE BOILERPLATE PRCUEINSTRUMENTED VHCE COMMAND PARAVEHCHUE CYLINDRICAL
MODULE TETVHCETEST VEHICLE
FIGURE 5-22- Drag Lous of the Apollo 16.5-Foot-Diameter, Ribbon
Drogue Chute Caused by Different Forebodies.
* 5-23
NWC TP 6575
-/ _ INFLATED PARACHUTE DIAMETER, D O
EFFECTIVE FOREBODY AREA, SB
EFFECTIVE FOREBODY DIAMETER, DB
77,
FIGURE 5-23. Determination of Effective Forebody Diameter.
5.2.3 Measured Drag Coefficients of Various Types of Parachutes
Drag coefficients are discussed in this section for solid flat, conical, triconical,
extended-skirt, hemispherical, annular, and cross parachutes. These data were calculated
from drop tests conducted over a period of time, primarily at the El Centro test facility. The
main source for determining rates of descent were phototheodolite measurements, although
some older tests used the 300-foot drop-line method. Most of the data were collected by the
author; the summary data in Figure 5-24 were plotted by E. Ewing of Northrop-Ventura and
presented in Figure 6-35 of Reference 2.1.
Figure 5-24 plots the measured drag coefficient data for solid, flat circular, circular
conical, triconical, extended-skirt, ringsail, annular, and ringslot parachutes. The data confirm
the previously stated fact that triconical, annular, and extended-skirt parachutes have the
highest drag coefficients. The data also confirm that, similar to model parachutes
(Figure 5-16), the drag coefficients of unstable, large parachutes decrease with increasing rates
of descent.
References 5.13 through 5.20 refer to solid circular flat, circular conical, and triconical
parachutes in general, and not to any specific parachute evaluated for the drag coefficient data
in Figure 5-24.
5-24
NWC TP 6575
0
1.1
"A A Av
1-" 0.9 z
U�LLU- 0.8__
0
" 0.7
0.6
0.5 - -
15 20 25 30 35 40 50 60 70 80 90
RATE-OF-DESCENT, Veo FPS (EAS)
PARACHUTE TYPE D0 . FT Le'Do
* SOLID FLAT CIRCULAR 24-28 0.75-1.0
9 SOLID FLAT C!RrCtJLAR 100 0.95-1.0
V SOLID CONICAL CIRCULAR 95-100 0.95-1.0
A TRICONICAL 79.6-100
-- 14.3% EXTENDED SKIRT 60-67.3 0-92-1.0
" 10% EXTENDED SKIRT 56-67.2 1.0
10% EXTENDED SKIRT MC-1 35 0.85
" 10% EXTENDED SKIRT 34.5-38 0.87-0.94
"--@-RINGSAIL (XT = 7-8%) 56.2-84.2 0.94-0.97
-'•"RINGSAIL OT = 72%) 88.1 1.4
* ANNULAR (Dv/Dp = 0.63) 42-64 1.25
FIGURE 5-24. Drag Coefficient Versus Rate of Descent for Various Types of
Solid Textile Parachutes.
* 5-25
NWC TP 6575
Extended-Skirt Parachutes. Figure 5-25 shows the drag coefficient versus rate of descent 0
for various types of extended-skirt parachutes. These data are the result of numerous tests
conducted with individual parachutes. The extended-skirt parachute was developed at
Lakehurst, New Jersey, by the U.S. Navy in the late 1940s (Reference 5.21). In 1952, the U.S.
Air Force used the extended-skirt design to develop the T-10 Troop Parachute (Reference
5.22). Extended-skirt parachutes designed for recovery of the Q-2 and the USD-5 drones
achieved high drag coefficients combined with reasonably good stability of about 10 degrees of
oscillation (References 5.23 and 5.24).
1.0
0.1 94!tA..~ YBL TP
C° LEGEND
-"0SYMBOL TYPE REF
Z 0.6 FT
10% ES 38 5.23 L 10% ES 34.6 6.22
o 0.4 0 FES 71 5,23 U
0 FES 78 523
A FES 67 5.24
0.2 0 FCES 28 5.2
A EXPER 36.4 5.2
0 10% ES 34.9 5.23
0.0I I
10 16 20 25 30 35 40 45
RATE-OF-DESCENT. Veo FPS
FIGURE 5-25. Drag Coefficient Versus Rate of Descent for Various
Extended-Skin Parachutes.
Combining the high drag effect of the triconical parachute with the good stability and low
opening shock characteristics of the extended skirt design may produce a parachute
combining the best features of both designs.
The sensitivity of extended-skirt parachutes to suspension-line length is shown in
Figure 5-26. These tests were conducted with an 11.8-foot-diameter, 10% extended-skirt
parachute in the Wright Field vertical wind tunnel. The data also demonstrate the effect of
velocity on the drag coefficient.
Cross Parachute. In recent years, the cross parachute has been used for aircraft and
ordnance deceleration as a low-cost replacement for the ringslot parachute. The cross
parachute was first tested in 1947 by the Naval Ordnance Laboratory (Reference 5.25) and was
reintroduced in 1%2 as the French cross parachute (References 5.26 and 5.27). The Naval
Surface Warfare Center (NSWC) at Silver Spring, Md., has conducted many aerodynamic and
5-26 0
NWC TP 6575
00
0.9-
S0.85-- . .
S0 Ve 20 FPS
,0 /Ve = 30 FPS
O 0.75.
0.65,±
'374
0.6 0.7 0.8 0.9 10 1.1 1.2 13 1.4
SUSPENSION-LINE-LENGTH RATIO, LeD 0
FIGURE 5-26. Effect of Suspension-Line Ratio on an
1.8-Foot-Diameter Extended-Skirt Parachute.
stress investigations on cross parachutes (References 5.28 to 5.32). NSWC is using the cross
parachute for the stabilization and retardation of mines, see section 8.6.4. Reference 5.33
describes the use of a cross parachute as a final descent parachute. Figure 5-27 shows the cross
parachute drag coefficient as a function of rate of descent evaluated from the NSWC
programs. This stable parachute increascs its drag coefficient witl a decreasing rate of
descent, a fact previously observed only on unstable parachutes. Drag znd stability of the cross
parachute depend on the arm's diameter-to-width ratio (W/L), on the number and length of
suspension lines, and on cloth porosity. To conform togeneral use, the nominal diameter, Do, is
used in this manual instead of the arm length to define cross parachute diameter. Reports
published primarily by the NSWC should be consulted before using this parachute.
Wind-tunnel and water-tank tow tests on cross parachutes were conducted by the University of
Leicester, England (Reference 5.34 and 5.35).
Annular Parachute. The annular parachute was developed in 1947 and named the airfoil
parachute (Reference 5.36). Figure 5-28 shows its high drag coefficient. The parachutes with
individual symbols in the figure are annular parachutes used in connection with a ringslot or
ringsail engagement parachute for midair retrieval systems (References 5.37 and 5.38).
Ribbon Parachutes. Section 5.8contains drag data on ribbon parachutes for the subsonic
and supersonic range. Ribbon parachute performance depends to a large extent on selection of
the right porosity. Design data, including the required porosity for a particular parachute size
and application, are discussed in Chapter 6. References 5.39 through 5.47, published by
various organizations, discuss performance, design details, and subsonic and supersonic
applications of ribbon parachutes.
5-27
NWC TP 6575
0.8 -9--o I® 1* *
0( 0 LD3
8 o.5
L~~~ 10"....
Z 0.6 FL /o - - - I
_____ LEGEND
TYPE Do, REFERENCE o SYMBOLS TEST FT
0.2 (0) 0 FFT 136 526
Q -- WTT 2.5 5 28/29
@ WTT 2.5 5.27
) FFT 613 5.33
0 _--1. 1
10 20 30 40 50 60 70 80
RATE -OF-DESCENT. V FPS
FIGURE 5-27. Drag Coefficient Versus Rate of Descent for Various Cross Parachutes.
12
*0
L) =LEGEND
0 SYMBOL O0 TYPE REF
< ~OF E oFT TEST
06 28 FFT 53•6
0 42 FFT 537
718 FFT 638
S • 84 FFT 67 FFT -
0 1o 15 20 25 30
RATE -OF-DESCENT. Vo FPS 0
FIGURE 5-28. Drag Coefficient Versus Ratc of Dcscent for Various
Annular Parachutes.
5-28
NWC TP 6575
"The influence of Mach number on the drag of ribbon-type drogue chutes is discussed in
section 5.8.
Ringslot Parachutes. References 5.48 and 5.49 give design details on ringslot parachutes.
A drag coefficient, CD0o, of 0.65 has been measured in free-fall tests. Selection of the proper
total porosity, in accordance with Chapter 6, is important. Ringslot parachutes used as landing
deceleration parachutes for aircraft experience a drag coefficient reduction from 0.65 to 0.60
because of the large wake behind the aircraft.
Rlngsail Parachutes. Reference 5.50 is a summary report on ringsail performance,
design, and application. These parachutes were used as the main descent parachutes for the
Mercury, Gemini, and Apollo spacecraft and for the ejectable crew module of the F-ill
aircraft.
Hemisflo Parachute. This supersonic ribbon parachute should be used at speeds of
Mach 2 or higher. References 5.51 and 5.52 provide information on the development, design,
and application of hemisflo parachutes.
Guide Surface Parachute. This parachute was developed as a high-stability, low drag
parachute for the stabilization of bombs, mines, and torpedoes. It combines good stability
with excellent damping characteristics. For details see References 5.53 and 5.54.
Disk-Gap-Band Parachute. Some information on this parachute, used successfully to
land the Viking spacecraft on the planet Mars, is contained in References 5.55 and 5.56.
Rolating Parachutes. Several types of rotating parachutes have been used successfully.
Angled vents in the parachute canopy rotate the parachute. Centrifugal forces acting on the
canopy and suspension lines increase the projected diameter, resulting in a high drag
coefficient. Attempts to use rotating parachutes with diameters greater than 10 feet have been
unsuccessful because of deployment and canopy wrap-up problems. References 5.57 through
5.59 provide information on the three best known types of rotating parachutes.
Maneuverable (Gliding) Parachutes. Maneuverable gliding parachutes and their
performance characteristics are discussed in section 5.9.
Balloon-'yype Decelerators. These deceleration devices, including the Goodyear ballute,
are discussed in section 5.8.
5.2.4 Effect of Reynolds Number on Parachutes
Chapter 4 states that parachutes, unlike airfoils, operate in turbulent flow because of the
separation of the airflow at the leading edge of the parachute canopy. For this reason, the
5-29
NWC TP 6575
Reynolds number does not appear to change the drag coefficient of parachutes. Measured
data on parachute drag coefficient versus Reynolds number are compared in Figure 5-29 with
the known Reynolds number effect on the drag coefficient of a sphere. These data are taken
from Reference 2.1.
S~CIRCULAR DISC
0 CIRCULAR DISC
C RIGID HEMISPHERICAL
Z ^. FABRIC HEMISPHERICAL
",' 3 1 CRUCIFORM
0• 3.79:1 CRUCIFORM
SPH-ERE
105 106
Re - vD i -
FIGURE 5-.19. Effect of Reynolds Number on Drag Coefficient for a
Sphere and Various Parachutes.
5.3 STABILITY OF PARACHUTE SYSTEMS
5.3.1 General Definition
Stability may be viewed as the tendency of a body to return to a position of balance or
equilibrium after a displacement from that pe.sition. Controllability may be defined as the ease
of causing that movement, or as the effectiveness of the mechanism us,,ed to cause the body to
return to its original position. Various concepts of stability can be illustrated by simple
examples. In Figure 5-30a, a ball is shown at rest in a concave depression. A displacement of
the ball will result in gravity restoring it to its original position. This state is called "stable." If
the ball is placed on a flat surface. a displacement of the ball from its position of rest will cause
the ball to come to Test at a different location on the flat plate, with no tendency for the ball to
return to its original position; this state is termed "neutrally stable" (Figure 5-30b).
Figure 5-30c shows a ball placed in a state of equilibrium atop a larger spherical ball. Clearly,
any displacement of the small ball on the large sphere causes the ball to continuously move
away from its original position of stability. This condition is termed "unstable." In the three
simpie examples, we have considered the conditions connected with static stability.
5-30
NWC TP 6575
(a) STABLE (b) NEUTRALLY STABLE (c) UNSTABLE
FIGURE 5-30. Illustration of Static Stability.
Dynamic stability refers to the continued motion of a moving body and may be illustrated
by considering the ball on the concave surface in Figure 5-30a. The friction forces on the ball
are always in a direction opposite to its motion. The friction forces, positive damping effect,
together with the gravity component, make the ball tend to oscillate with a decreasing
amplitude until it finally achieves the illustrated position of static stability. A ball in this
dynamic environment is called "dynamically stable." If the aerodynamic forces of air
resistance and the mechanical frictional forces could be reduced to zero-an impossible
condition-there would be no damping force on the ball, and a small displacement of the force
applied to the ball would cause an indefinite oscillation of constant amplitude. Such a
condition is termed "neutrally dynamically stable." If friction force is overcome by some
external force-for example, a propulsion force-the ball would oscillate with an increasing
amplitude and would not return to its position of equilibrium; this condition is called
"dynamically unstable."
These conditions of dynamic stability are graphically illustrated in Figure 5-31, which
demonstrates the stability of three bodies. Body "a" is dynamically and statically unstable.
Body "b" is statically stable but dynamically unstable, resulting in ever-increasing oscillations.
Body "c" is dynamically and statically stable, resulting in oscillations dampened with time.
The fact that a body is statically and dynamically stable is frequently not sufficient. For
example, an automobile without shock absorbers is statically and dynamically stable in its
spring motions, but may provide an uncomfortable ride because of insufficient damping of its
body oscillations. Installation of shock absorbers increases positive damping and causes a
rapid decrease of the body oscillations with time, thereby providing a comfortable ride.
5-31
NWC TP 6575
z
0
t a
0
•5_b =e STBEUSAL
2 TIME 0
U. \Z
W STATICALLY DYNAMICALLY
a = UNSTABLE UNSTABLE
b - STABLE UNSTABLE
c = STABLE STABLE
FIGURE 5-31. Graphical Illustration of Dynamic Stability.
A statically stable parachute may require excessive time to decrease its oscillation after
an external disturbance, such as a wind gust, indicating that the parachute's damping
characteristics are inadequate for stabilizing an unstable body.
In the case of an aircraft, good static and dynamic stabilities are desirable for large
cargo-type aircraft, but this stability counteracts fast changes in attitude and position required
for fighter aircraft, which are generally built with low or neutral static stability. In recent years,
aircraft requiring a high degree of mobility have been designed with a slightly negative static
stability, thus increasing mobility and decreasing the size and drag of the control surfaces.
S.3.2 Parachute Stability
Stability is defined as the tendency of a body to return to a position of equilibrium after
displacement. Parachute engineers frequently use the term stability loosely. If two airdrop
platforms descend, each on a 100-foot-diameter parachute, and one parachute oscillates * 30
degrees and the other ± 5 degrees, observers frequently call the former parachute system
unstable and the latter stable. In reality, both parachute systems are statically unstable in the
oscillating mode but are sufficiently dampened dynamically to stay within their ranges of
oscillation without increasing the oscillation amplitude. It is more precise to define these
parachutes as oscillating ±30 degrees or ± 5 degrees; and, if possible, to state that
5-32
NWC TP 6575
0 disturbances such as those caused by wind gusts are dampened within a given number of full
oscillations. The parachute oscillating + 5 degrees most likely meets the requirements for
airdrop; however, the same parachute is unsuitable for stabilizing airdropped bombs or
torpedoes. For this application, a parachute with zero oscillation and good damping is
required. As defined later in this section, a parachute meeting this requirement has a steep
negative dC./dc over a wide range of angles of attack.
Why should one parachute have no oscillation and strong damping characteristics while
another parachute oscillates violently? Figure 5-32 explains this difference by showing the
airflow around several types of parachute canopies and rigid hemispheres. The airflow, made
visible with smoke ejected from equally spaced nozzles in front of the parachute models, acts
as streamlines, as explained in Chapter 4. Figure 5-32a shows the airflow around an imporous
hemisphere. Airflow cannot get through the canopy but goes around and separates on the
leading edge of the hemisphere in alternating vortexes, forming what is called the Karman
-------------------------- / ,-
KARMAN VORTEX
TRAIL
-- . .... M- ---(SOLID CIRCULAR)_
N 8
ATTACHED FLOW IN
(A) IMPOMOUS CANOPY. INSTAGILITY CAUSRO 9V SIDE PONCI. N. ft
FLOW SEPARATION (d) POAOUSCANOPY. STABILIZING MOMENT, 0 * A * N ft *
.2 • UNIFORM
- . .. --. , WAKE LARGE PROJECTED AREA _ (RIBBON)
FLOW SEPARATION DRAG 0
(I) POROUS CANOPY. NO SDoE FORC1. NO UN&TAILE MOMCMT. -A
•_ FLIOý% SEPARATION M) CANOPY WITH SCOIAMAAION 9001, STAWlLIZlNO MOhMINT,
-FLOVV SEPARATION
Ic) CANOPY WITN SEPARATION LOGE (OGUIOD URFAC1).
No SIOID POAC. NO UNITABLe MOMENT.
FIGURE 5-32 Relationship of Airflow and Stability for Various Parachutes.
0 5-33
NWC TP 6575
Vortex Trail. The separation causes alternate pressure areas on opposite sides of the canopy,
and these pressure areas produce the parachute's oscillations.
Figure 5-32b shows the effect of openings in the canopy. Part of the air flows through the
canopy and forms a uniform wake consisting of small vortexes. In addition, the airflow
separates uniformly around the leading edge of the canopy, eliminating the destabilizing
alternate flow separation of the Karman Vortex Trail. Uniform wake and airflow separation is
the principle of the ribbon parachute and all slotted parachute canopies.
The guide surface parachute (Figure 5-32c) has a sharp separation edge around the skirt
of the canopy, creating a strong, uniform airflow separation around the leading edge. In
addition, the inverted leading edge (guide surface) creates a large, stabilizing normal force.
Both the normal force, N, and the drag force, D, create a stabilizing moment if the parachute is
displaced from its zero-angle-of-attack position (Figure 5-32e). The known main design
features for creatingstable parachutes are uniform airflow separation around the leading edge
of the canopy, airflow through the canopy, and a large restoring moment such as that generated
by a guide surface.
The static stability of various parachutes has been measured numerous times in
wind-tunnel tests. Figure 5-33 plots the moment coefficient of several parachute types and of
rigid hemispheres, as measured by the University of Minnesota (References 5.60 and 5.61). A
negative dCm/da of the moment coefficient curve indicates that the parachute is stable and
will return to its zero-angle-of-attack position after a disturbance. The solid, flat. circular
canopy is a typically unstable parachute. It will oscillate between k 25 degrees, but if deflected
more than 25 degrees it will return to the 25-degree position. The ribbon and guide surface
parachutes will return to their zero-angle-of-attack attitude if displaced, as indicated by the
negative slope of the dCm/dct curve going through the zero-angle-of-attack position for both
parachute types.
The guide surface parachute has the steepest dCm/dc, and, therefore, the strongest
stabilizing moment and best damping characteristics of all known parachutes.
Larger parachutes oscillate less than small parachutes. A 3-foot-diameter solid flat
circular parachute manufactured from standard 1.1-oz/y 2 ripstop material, tested in a wind
tunnel, will oscillate about ± 35 to 40 degrees. The standard 28-foot-diameter personnel
parachute oscillates about ± 30 to 35 degrees. The 100-foot-diameter G-11 cargo parachute
oscillates about 10 to 20 degrees. The 200-foot-diameter cargo parachute manufactured from
1.6-oz/y 2 material with about the same porosity as the other parachutes (described in
Reference 5.14) oscillates less than 5 degrees. Ludtke discusses oscillation problems in
Reference 5.62.
5-34 0
NWC TP 6575
RIGID HEMISPHERE WITH
35% GEOMETRIC POROSITY
0.4
GUIDE SURFACE PARACHUTE
NOMINAL POROSITY:
100 FT 3 /FT 2 /MIN
0.3
E
1-: 0.2 SOLID FLAT PARACHUTE
Z NOMINAL POROSITY:
2_ 100 FT 3
/FT 2 /MIN
U.
ILLU
0
L) 0.1
I�z
0
+
RIGID HEMISPHERE
0.1 NONPOROUS RBO AAHT
Cm RELATED TO PROJECTED 28%BO GEMERICALT
AREA AND MOMENT CENTER POROSITY
1.33 D P BELOW CANOPY SKIRT
I I I I I I I I I 1
-70 -60 -50 -40 -30 -20 -10 +10 +20 +30 +40 +50
ANGLE OF ATTACK,a, DEGREES
NOTE: IN THE U.S. A STABILIZING MOMENT IS DEFINED
AS HAVING A NEGATIVE dCm/da. IN EUROPE, A
STABILIZING MOMENT IS DEF:NED AS HAVING
A POSITIVE dCm/da.
FIGURE 5-33. Moment Coefficients Versus Angle of Attack for Guide Surface; Ribbon;
and Flat, Circular Parachutes; and for Porous and Nonporous Hemispheres.
0 5-35
NWC TP 6575
5.3.3 Stability of a Parachute Body System
Parachutes that are used with stable air vehicles must also be stable and not interfere
with the inhercnt stability of the vehicle. Parachutes with good stability and high drag are used,
such as the ribbon, ringslot, and cross parachutes. If a fast-falling, unstable body must be
stabilized while maintaining a high rate of descent, a parachute with a strong negative
dCm/do,, such as a guide surface parachute, may be preferable. For each parachute assembly,
a compromise between required stability, weight, volume, and cost determines the final
selection.
The following parachute application ranges have been established based on many years
of practical experience.
Aircraft Landing Deceleration. Aircraft are inherently stable and do not require aircraft
landing deceleration parachutes to contribute to their stability. Therefore, high drag stable
parachutes that do not interfere with the aircraft controllability are used. Ribbon, ringslot, and
cross parachutes are used primarily for aircraft landing deceleration.
Bomb Stabilization. During World War II, the Germans developed parachute-stabilized
bombs that enabled them to shorten the length of the bomb and to store more bombs in
existing aircraft bomb bays. These fast-falling bombs required a low drag, highly stable
parachute with good damping capability to obtain the desired stability. The guide surface
parachute was developed specifically for this application as a low drag, high-stability
parachute (Reference 5.53). A single riser attachment did not provide a sufficiently stable
parachute-bomb system, and a more rigid connection between the bomb and the parachute
was required. Figure 5-34 contains two examples of rigid parachute-bomb connections: the
multiple-point attachment on the circumference of the bomb and the geodetic attachment.
The geodetic attachment is the best solution but is more complex.
Torpedo and Mine Stabilization. Mines and torpedoes that are airdropped from low
altitudes are equipped with retardation parachutes to
1. Decelerate the store to an acceptable water entry velocity, generally below 200 ft/s.
2. Obtain a water entry angle that avoids ricochet.
3. Avoid store oscillation and associated store damage at water impact.
Guide surface, ribbon, ringslot, and cross parachutes are being used successfully for this
application.
Bomb Retardation. Bombs dropped at high speeds from low-flying aircraft must be
retarded to
1. Obtain a steep impact angl, to avoid ricochet.
2. Permit the aircraft to escape the effective range of the exploding bomb.
3. Obtain a good fragmentation pattern associated with a steep impact angle.
5-36 0
NWC TP 6575
S
BOMBS
(a) SINGLE POINT (b) MULTIPLE POINT (c) GEODETIC
* AIRCRAFT CREW MODULES
(d) CENTER LINE (e) MULTIPLE POINT (f) SINGLE POINT
CG ATTACHMENT CG ATTACHMENT
FIGURE 5-34. Various Conrigurations of Parachute Vehicle Attachments.
5 5-37
NWC TP 6575
Stable parachutes with good drag characteristics used for this one-time application
include ribbon, ringslot, and cross parachutes as well as the inflatable ballute-type retarders.
Fjection Seat, Encapsulated Seat, and Crew-Module Stabilization and Retardation. All
three aircraft escape systems need parachutes for stabilization and retardation. Stabilization
is required in pitch, yaw, and roll; parachutes can provide stabilization in pitch and yaw, but
are poor for roll control. For descent from a high altitude, a roll control of not more than 2 to 3
rpm is necessary for aviator comfort. This control can be obtained with a relatively large
drogue chute with an equivalent sea-level rate of descent of 120 to 150 ft/s.
The aircraft crew-module stabilization in Figure 5-34 demonstrates the problem of
stabilizing an asymmetrical body with the center of gravity (CG) off the center line of the
vehicle. In the example shown, the drogue chute had to be attached offset to the nose section of
the XS-2 research aircraft to ensure that the parachute force line would run through the CG of
the crew module with the module hanging at a -2 degree zero lift attitude to eliminate
destabilizing side forces (Reference 5.11).
The stability relationship of parachute and forebody is quite complex in systems where
unstable forebodies must be stabilized by minimum size parachutes. Both the forebody and
the parachute can oscillate in a 360-degree plane. The stability of such two-body,
multi-degree-of-freedom systems has been investigated by several authors (References 5.63
through 5.67).
Neustadt showed that deploying a parachute opposite the oscillating motion of the
forebody may increase the parachute force by as much as 20% (Reference 5.68).
S.4 PARACHUTE INFLATION PROCESS
5.4.1 Opening Force Investigations
Many attempts have been made to develop theoretical solutions to the parachute
inflation process and obtain quantitative values for opening time and force. Investigations by
Mueller, Scheubel, O'Hara, Rust, Heinrich, Wolf, and Purvis, defined in References 5.69
through 5.75, have increased the understanding of the parachute opening process, including
the effect of apparent mass. However, no satisfactory practical solution for calculating filling
time and parachute opening forces has evolved. The analytical solution of the opening process
has been complicated in recent years by the development of means for controlling parachute
inflation, such as reefing, sliders for steerable parachutes, pull-down vent lines, and related
devices. While these methods provide control of parachute inflation, and thereby the opening
forces, they also interfere with the parachute's natural inflation process. A good account of the
present status of the parachute inflation theory was presented by D. Wolf in 1982 during the
University of Minnesota Short Course on Parachute Systems Technology (Reference 2.17).
5-38
NWC T? 6575
In 1942 Pflanz developed a numerical method for calculating parachute opening forces
(References 5.76 and 5.77). He assumed that the drag area of the parachute or of any drag
device increased from a low value to 100% in a given time and in a mathematically definable
form, such as convex, concave, or linear. The parachute filling distance was assumed to be
constant for a specific parachute. The Pflanz method includes altitude effects but does not
include gravity effects or drag area overshoot after full opening.
Schuebel was the first to investigate the effect of the apparent mass on the parachute
opening process. He defined apparent mass as both the air mass inside the inflating canopy
and the air mass outside the canopy that is affected by the inflation process (Reference 5.70).
Modern, high-speed computers make it possible to calculate the time-dependent
force-velocity-trajectory history of the parachute opening process for complex recovery
systems. This calculation was first accomplished in 1960 by Space Recovery Systems, Inc.
(Reference 5.23). The computer results agreed well with the forces measured in free-flight tests.
This force-velocity-trajectory approach was used in an extended form for predicting the
parachute opening forces of the Gemini and Apollo drogue and main parachutes (References
5.78 and 5.79). McEwen gives an excellent review of previous efforts and recommends that
inflation distance, not inflation time, be used as the reference for the inflation process.
For a parachute-vehicle system moving in space (Figure 5-35), the trajectory equations
can be written in the form shown in the figure.
dv -F-Dr +Wv SINO
dt My
dO -g COS 0
dt V
(F + DO)
FIGURE 5-35. Angle and Force Relationships for a Deceleration
System Moving in Space.
The parachute force, F, as a function of time is
(m + m p)4 dv - +v- dm, + WvsinO
(CDS)pp/2v 2 + -mp)
5-39
NWC TP 6575
where
F - parachute force acting parallel to the flight trajectory, lb
D, - drag of the vehicle (payload), lb
Wv - weight of the vehicle or payload, lb
0 - trajectory angle against the horizontal, degrees
S - deceleration of gravity, ft/s2
(CDS)p - parachute drag area, ft2
p - density of air, slugs/ft3
v = trajectory velocity, ft/s
ma - apparent mass (added mass), slugs
mp = mass of parachute, slugs
mv - mass of the vehicle or payload, slugs
Wp = weight of the parachute, lb
The drag of the vehicle, Dr, depends on the drag area of the vehicle and on the
instantaneous dynamic pressure, which changes during the opening process of the parachute.
The trajectory angle, 0, changes from the launch or deployment angle to vertical most
rapidly during and after urachute inflation.
Changes in the value of the acceleration of gravity, g, do not affect the outcome at
altitudes below 100,000 feet.
The parachute drag area, (CDS)p, increases from close to zero at line stretch to 100% at
full open canopy.
Density, p, changes with altitude; this change must be considered for longer trajectories.
Both parachute and payload are assumed to have the same velocity and the same trajectory
angle.
The apparent or added mass, ma, is calculated by multiplying volume by density and by a
form factor that depends on the particular parachute type. The apparent mass at an altitude of
40,000 feet is only one-quarter of the apparent mass at sea level, because apparent mass
depends on density. Therefore, the apparent mass affects the magnitude of the parachute
opening force at a given altitude.
5-40
NWC TP 6575
0 In the parachute force equation, the vehicle weight is Wv • sin 0. Using the sign
convention of Figure 5-35, a parachute opening in a vertical attitude will have a force that is one
unit weight higher than the force of a parachute opening in a horizontal attitude. This force
difference must be considered in planning parachute test programs.
5.4.2 Parachute Canopy Inflation
Parachute inflation is defined as the time interval from the instant the canopy and lines
are stretched to the point when the canopy is first fully inflated. Figure 5-36 shows the phases of
canopy inflation. The canopy filling process begins when canopy and lines are stretched and
when air begins entering the mouth of the canopy (a). After the initial mouth opening, a small
ball of air rushes toward the crown of the canopy (b). As soon as this initial air mass reaches the
vent (c), additional air starts to fill the canopy from the vent toward the skirt (d). The inflation
process is governed by the shape, porosity, and size of the canopy and by air density and
velocity at the start of inflation. Inflation is slow at first but increases rapidly as the mouth inlet
of the canopy enlarges (e) and the canopy reaches its first full inflation (f). Most solid textile
canopies overinflate and partially collapse because of the momentum of the surrounding air
(g). Several factors contribute to an orderly, repeatable inflation process and to a low, uniform
(a) OPENING OF CANOPY MOUTH
* (b) AIR MASS MOVES ALONG CANOPY
S(c) AIR MASS REACHES CROWN OF CANOPY
(d) INFLUX OF AIR EXPANDS CROWN
(TYPICAL REEFED INFLATION SHAPE)
(e) EXPANSION OF CROWN RESISTED BY
STRUCTURAL TENSION AND INERTIA
if) CANOPY REACHES FIRST FULLY INFLATED
STAGE
(g) SKIRT OVER-INFLATED, CROWN DEPRESSED
BY MOMENTUM OF SURROUNDING AIR MASS
FIGURE 5-36. Parachute Canopy Inflation Process.
0 5-41
NWC TP 6575
opening force. The amount of air moving toward the canopy vent at point (b) should be small to
avoid a high-mass shock when the air bubble hits the vent of the parachute. The inflation of the
canopy should occur axisymmetrically to avoid overstressing individual canopy parts.
Overinflation of the canopy after the first initial opening should be limited to avoid delay in
reaching a stable descent position.
Methods have been developed to control the inflation of the canopy; the most frequently
used is canopy reefing. Reefing stops the inflation of the canopy at one or more steps between
stages (c) and (0), thereby limiting the parachute opening force to a preselected level.
Retfing is also required for uniform inflation of parachutes in a cluster. Stopping the
inflation of all cluster parachutes at a point close to stage (d) of Figure 5-36 allows all
parachutes to obtain an initial uniform inflation-a prerequisite for a uniform final
inflation--without running into a lead/lag chute situation with widely varying parachute
forces. Other means for controlling the parachute opening include ballistic spreader guns,
sliders for gliding parachutes, and pull-down vent lines.
5.4.3 Canopy Inflation Time
Knowledge of the canopy filling time, defined as the time from canopy (line) stretch to the
first full open canopy position, is important. Mueller and Scheubel reasoned that, based on the
continuity law, parachutes should open within a fixed distance, because a given conical column
of air in front of the canopy is required to inflate the canopy (References 5.69 and 5.70). This
fixed distance is defined as being proportional to a parachute dimension such as the nominal
diameter, DO. This assumption was reasonably confirmed in early drop tests with ribbon
parachutes. French and Schilling, in papers published in 1968 and 1957, confirmed this
assumption (References 5.80 and 5.81). Using the fixed-distance approach and the definitions
in Figure 5-37, the filling distance for a specific parachute canopy can be defined as
sf = n Dp - constant.
With sf = n DP` the canopy filling time, tf, can be defined as shown in Figure 5-37.
sf = n D P
FIGURE 5.37. Filling Distance of a Parachute Canopy.
5-42 0
NWC TP 6575
Because the parachute diameter, Dp, is variable, the fixed nominal diameter, Do, is used
to calculate canopy filling time
n D.
V
where
Do is the nominal par,,iiute diameter, feet
v is the velocity at line stretch, ft/s
n is a constant, typical for each parachute type, indicating the filling distance as a
multiple of Do, dimensionless.
The constant, n, will be called "fill constant" in subsequent discussions. The basic
filling-time equation, tf - n Do/v, has been extended by Knacke, Fredette, Ludtke, and others.
The following formulations have provided good results.
Ribbon Parachute
tf- D•.
where n - 8 (Knacke).
This equation gives accurate results with ribbon parachutes when the canopy porosities
recommended in Chapter 6 are used. For small-diameter ribbon parachutes investigated in
high-speed sled and rocket tests, Fredette found the following relationship:
tf = 0.65ATDo v
where XT is the total canopy porosity expressed as a percent of the canopy surface area, So.
Solid Flat Circular Parachute
Wright Field investigations resulted in the following formulations:
nDo tf M= n-D V0.85
where n - 4.0 for standard porosity canopig, and n = 2.5 fe. low porosity canopies.
0 5-43
NWC TP 6575
Cross Parachute
An investigator at NSWC, Silver Spring, Md., recommends
. (CDS)pn
where n - 8.7. The author has evaluated parachute fling-time data from free-flight tests and
found that a formulation for filling time, where the line-stretch velocity, vs, is a linear function
instead of an exponential function, gives satisfactory results in the medium-velocity range of
about 150 to 500 ft/s. Table 5-6 lists the fill constant, n, in the equation tr -nD for a variety of v
parachutes.
TABLE 5-6. Canopy Fill Constant, n, for
Various Parachute lypes.
Canopy fill constant, n
Paraxe type Res DWW Unreeofe
opening opening opening
Solid flat circular ID& ID a
Extended-skIrt, 10% 16-18 4-5 10
Extenled-skirt, full 16-18 7 12
Cross ID ID 11.7
Ribbon 10 a 14
Ringslot ID ID 14
Rlngsall 7-8 2 7
Ribless guide suudace ... ... 4-6
a ID = Insufficient data available for meaningful
evaluation.
Additional fill-factor data can be found in Table 6-1 of Reference 2.1.
The filling time of the various stages of reefed parachutes can be determined as follows:
Do (CDS)R 1and t 5-4 - nD (CDS)o - (CDS)R 1/2
Vs (CDs), Vt (CDS)o
5-44
NWC TP 6575
where
tf, and tf2 are the reefed and disreefed filling times,
vs and Vr are the velocities at line stretch and at disreef, ft/s
(CdS)R and (CdS)o are the reefed- and full-open drag areas, ft2.
Some solid textile, circular parachute types appear to have a critical opening velocity. At
high velocities and high dynamic pressures, the canopy opens only partially. The drag of the
partially opened parachute decelerates the parachute-vehicle system and the canopy opens
fully. This type of opening can also occur on ribbon parachutes with porosities that are too
high (Figure 6-23). Attempts to use this phenomenon for controlling the canopy inflation
process, and thereby the parachute forces, have not been successful because of the variables
involved and the difficulty of controlling the porosity of solid fabric canopies.
Some types of ribbon parachutes have been opened in the velocity range of up to Mach
4.0. Greene concludes that canopy filling time at supersonic speeds is constant, because the
canopy operates behind a normal shock. Reference 5.82 presents test data that appear to
confirm his investigations.
In a NASA test program to develop parachutes for planetary landing, ringsail, cross, and
disk-gap-band parachutes were opened successfully at altitudes above 100,000 feet and at
speeds exceeding Mach 3.0. Section 5.5 provides further details on high-altitude effects, and
section 5.8 describes supersonic parachute applications.
5.4.4 Parachute Drag-Area Increase During Canopy Filling Process
The parachute drag area, (CDS)p, increases from 0 to 100% during canopy inflation. The
drag-area-versus-time increase--linear, convex, concave, or random-is well known and has
proven to be constant and repeatable for known parachute types (see Figure 5-38).
The drag-area-versus-time increase for reefed ribbon, ringsail, and extended-skirt
parachutes is shown in Figure 5-39.
RIBBON RINGSLOT CIRCULAR EXTENDED
1 7
l - , . k- t - tf1- t
FIGURE 5-38. "lypical Drag-Area-Versus-Time Increase for Various Parachute ypos.
5-45
NWC T? 6575
RIBBON EXTENDED RINGSAIL
C./1/1 /
,, I - I I.. . ,
FIGURE 5-39. lypical Drag-Arca-Verws-Time Increase for Reefed Parachutes.
The shape of the drag-area-versus-time curve may be somewhat drawn out or
compressed by reefing, changes in porosity distribution in the canopy, wide slots, or other
means; however, the basic configuration of the curve is maintained for a particular type of
parachute.
Drag-area-versus-time curves are obtained from wind-tunnel or free-flight tests by
dividing the measured instantaneous force by the instantaneous dynamic pressure. This, more
precisely, should be called a dynamic drag area, because it includes characteristics that affect
the opening process, such as apparent mass and altitude density.
The evaluated drag-area-versus-time increase for unreefed, solid flat circular, ringslot,
and personnel guide chutes (Figure 5-40), is taken from Reference 5.83. The author has added
the typical drag-area increase for ribbon and extended-skirt parachutes, determined from
numerous tests. Ribbon and ringslot parachutes have a strictly linear drag-area-versus�time increase, and solid textile parachute types have a rather uniform, concave form of
drag-area increase. Ludtke found that this increase of solid textile parachutes could be
expressed by
(CDS)X r I
(CIDS), Vf
where q is the ratio of the projected mouth area of the canopy at line stretch to the projected
frontal area of the fully opened canopy.
Figure 5-41 plots drag-area increase for the 63-foot-diameter reefed ringsail main
parachutes used with the Mercury space capsule. It shows a typical characteristic of ringsail
parachutes-the increase in drag area during the reefed stage. The ringsail parachute inflates
rapidly into an initial reefed stage and then grows slowly through inflation of additional rings.
This characteristic is advantageous for single parachutes because it constitutes a form of
continuous disreefing, a highly desirable feature.
5-46
NWC 1? 6575
20
0 1
I S PERSONNEL GUIDE SURFACE
o RINGSLOT CANOPY
L ELLIPTICAL CANOPY
1.6 0 SOLID FLAT CANOPY
o 10% EXTENDED SKIRT
1.4 V RIBBON
o 1.2
0.."
0/
Deo
002
0.
Ii
0.GUR 5c40 DrgAe.atoVru/imninesFiln ie
• ' / 0
g , /
0.4/ / /
000
0 0.2 0.4 06 08 1 0 1.2 14 1
t, t
S~FIGURE 5.40. Drag-Area Ratio Versus Dimensionless Filling Time.
400- 2000
A = POINT OF MAXIMUM REEFED FORCE
B - POINT OF MAXIMUM DISREEF FORCE
300 N
E,
1 ISREEF, I SCALE .
1400 2000
0 -
A
w
300 10 2
,R 5 a o i 200 1000
uJIU
0 O 20 30 40 50 60 70 80 9L
TiME SECONDS
FIGURE 5-41. Drag-Area-Venus-Time Diagram for the Mercury 64-Foot Ringsail Parac'hute.
0 5.47
NWC TP 6575
Figure 5-41 also demonstrates the extremely short disreefing time of 0.8 second.
References 5.50 and 5.79 include figures that show the drag-area increase for a single 85-foot�diameter Apollo ringsail main parachute. The increase in drag area during the reefed stage
proved detrimental for the cluster of the three Apollo main parachutes because it tended to
support nonuniform inflation.
Reference 5.23 gives drag-area-versus-time data for reefed, extended-skirt parachutes.
Several Sandia Reports (References 5.41 to 5.47) provide data on ribbon parachutes.
Drag-area-versus-time increase for a 101-foot-diameter, triconical parachute is shown in
Figure 5-42. The drag area in the reefed stage remains constant, which is typical for all known
types of parachutes except the ringsail. As shown in Figure 5-40, the disreef drag-area curve
displays the same concave shape as other solid textile parachutes. The triconical parachute, in
contrast to the ringsail parachute (Figure 541), has a long disreef time (tf2 = 7.5 seconds),
resulting in a relatively small canopy overshoot.
Data on drag-area-versus-time increase for the various parachute types are important
for establishing the drag-area-versus-time diagrams required for the force-time-trajectory
computer program described in this section and used in Chapter 7.
360 9000
F
320- -P 8000 -F
SREEFEDu 280 - 7000 -IREEF 1 wu 13 DISREEF cc
S240 - 6000 ,
S200- 5000 o -
Q 160- 4000 - .L_
wr U I "0120- ` 3000 -
"LL so- 0 2000
40- 1000- tr SEC- - f2
O 0 I I _
0 2 4 6 8 10 12 14 16 18 20 22 24
TIME, SECONDS
FIGURE 5-42. Drag-Area-Versus-Time Diagram for a Reefed
101-Foot-Diameter Triconical Parachute.
5-48
NWC TP 6575
Recovery system engineers should evaluate and publish drag-area-versus-time diagrams
to improve the database for computing the force-trajectory-time analysis of parachute
recovery systems.
S.4.5 Effect of Canopy Loading, W/(CDS)p, on Parachute Opening Forces
Figure 5-43 is a force-time diagram of a parachute opening in a wind tunnel. This pattern
is typical for parachutes without velocity decay during parachute inflation and is called the
"infinite mass" condition, because the parachute acts as if it were attached to an infinite mass.
The same parachute dropped from an airplane and weighted for a 20 ft/s rate of descent
will have the known force-time diagram of a personnel parachute (Figure 5-44).
The personnel parachute dropped from an airplane has a finite load and is referred to as
being tested, or used, under a "finite mass" condition. The primary difference between infinite
and finite mass conditions is that, under infinite mass conditions, the velocity does not decay
during parachute opening; whereas, under finite mass conditions, the velocity during
• "-Fx /Fc
F S Cx = Fx xl Fc
FIGURE 5.43. Parachute Force Versus Time for a Wind-Tbnnel Test (Infinite Ma&.- Condition)
/Fx
FIGURE 5.44. Force Versus Time for a Personnel
Parachute Drop (Finite Mass Condition)
"-49
NWC TP 6575
parachute opening decreases substantially. Infinite and finite mass conditions can also be
defined as conditions of high and low canopy loading, W/(CDS)p.
An additional typical difference between infinite and finite mass conditions is the
location of the peak opening force, F.. For a parachute opened under infinite mass conditions,
or high canopy loading, peak opening force occurs at the first full canopy inflation. The peak
opening force of a parachute opened at a finite mass condition will occur long before the
parachute canopy is fully open.
The relationship of the peak opening force, F., to the steady-state drag force, F., in
wind-tunnel tests is defined as
Opening-force coefficient, C, , = (see Figure 5-43).
C, is a constant for a specific parachute type, as shown in Tables 5-1 through 5-5.
With the newly defined opening-force coefficient, C,,, the equation for the parachute
force can be written
F, = (CDS)p q Cx X,
where
(CDS), = the drag area of the fully open parachute, ft2
q = the dynamic pressure at line (canopy) stretch, lb/ft2
C,- = the opening force coefficient at infinite mass, dimensionless
X1 = opening-force-reduction factor, dimensionless.
The force-reduction factor, X1, is 1.0 for a parachute opened at the infinite mass
condition; close to 1 for high canopy loading drogue chutes (close to the infinite mass
condition); and as low as 0.02 for final descent parachutes with a low canopy loading (finite
mass).
Table 5-7 shows the difference in opening forces and X1 factor for a 28-foot-diameter
parachute opened at 180 KEAS behind an aircraft as a landing deceleration parachute; behind
an ordnance device such as a bomb, mine, or torpedo for retardation; and as personnel
parachute for an aviator. The difference in the force reduction factor X1 for the three
applications is surprising. The primary reason for this effect is the difference in velocity decay
during the parachute opening process.
Figure 5-45 shows the force-time record of a 15.6-foot-diameter ringslot parachute
opened behind a B-47 bomber at a 30,000-foot altitude. This parachute, used as an approach
brake for descent from high altitude, has a canopy loading close to infinite mass condition,
resulting in an X, factor of 1.0.
5-50
NWC TP 6575
TABLE 5-7. Opening Forms and Canopy Loading of a 28-Foot-Diameter
Parachute for Various Vehicle Applications.
Vehicle Mass
AppliCatkon welght, Ib (CoS)P, ftz W/(C0 S)P, llMft 2 Cx Fl, Ib X, condition
Aircraft 140,000 490 286 1.7 91,200 1.0 Infinite
Ordnance 2000 490 4.1 1.7 30.100 0.33 Intermedlate
Petonnel 250 490 0.51 1.7 2900 0.032 Finite
180 9000 AIRSPEED
160 8000 x
Fx =7,400 LB•._
140 - 7000 -
u, 120 0 6000- F 6,800B
5 z B-47 APPROACH PARACHUTE 100- 0 5000-
0. TEST DATE: 5 MARCH 1954
I- . 15.6-FT-DIA RINGSLOT PARACHUTE
Q 80 - 4000 - DEPLOYMENT ALTITUDE. 30.000 FT 0 Cr "J 0 AIRCRAFT WEIGHT 128.000 LB
60- -- 3000 NCANOPY LOADING W (CD'S)o 2 1365 PSF
I F. = 7,400 L8, F, - 6.800 LS
40 - 2000 - F Cx .• 1 088, x I - 1.0
7-c
20- 1000 tf -- CDo .49
0 0 oF_ __ __I _I _ l 1 2 3 4 5 6 7
TIME AFTER COMPARIA -.NT DOOR OPENING, SECONDS
FIGURE 5-45. 15.6-Foot-Diameter Ringplot B-47 Approach Parachute Opening Forces.
The clean, aerodynamic configuration of the B-47 bomber produced a shallow approach
angle, making a point landing difficult. A 15.6-foot-diameter ringslot parachute was used
instead of wing brakes or spoilers to increase the drag on approach and thereby steepen the
glide angle. At touchdown, a 32-foot-diameter ribbon parachute was deployed as a
deceleration parachute side-by-side with the ringslot parachute. Deploying the parachutes at
even skirt levels assured successful opening of the second parachute. Note that the aircraft
velocity does not decay during parachute inflation.
Figure 5-46 shows the opening process and the opening force versus time for a
29-foot-diameter, guide surface personnel parachute tested at 250 knots at the El Centro,
Calif., whirl tower. The difference in the force-versus-time diagram, with the ringslot
0 5-51
NWC TP 6575
LEGEND
A = DROP
8 z CANOPY LINE STRETCH. F,
C = MAXIMUM PARACHUTE FORCE. F 3.740 LB
D CANOPY HALF INFLATED
E = FIRST FULL CANOPY INFLATION
4,000
C
3.000
2.,2000
0
UIf
0.1 0.2 0.3 04 05 06 0.7 08 09 10 TIME. 11 SEC1.2 1.3 1.4 15 16 17 18 1.9 20 21 22
FIGURE 5-46. Opening Proess and Opening Forme Venus Time for a Guide Surface Personnel Parachute
Tested at the El Centro Whirl Tower at 250 Knots With a 200-Pound Torso Dummy.
parachute opened behind the B.47 aircraft, is obvious. The maximum opening force, F1,
occurs when the parachute canopy has reached about one-third of its inflated diameter. The
force at full open canopy has decreased to about 600 pounds, indicating that parachute
velocity during opening has decreased almost to equilibrium velocity. The velocity decay
during opening results in an opening-force-reduction factor, X1. of 0.0239.
Another important characteristic is the relative size of the snatch force. On high canopy
loading parachutes, where the parachute mass is small compared to the mass of the vehicle to
be decelerated, the snatch force is small if the deployment system is good, as described in
Chapter 6. On low canopy loading parachutes, where the mass of the parachute can be 3 to 7%
of the mass to be decelerated, the snatch force can reach or surpass the maximum opening
force unless a proper deployment method is used.
All parachute applications fall into distinctive groups of canopy loading, W/(CDS)p.
Canopy loading is equivalent to dynamic pressure at equilibrium velocity and therefore relates
to rate of descent. Figure 5-47 shows this relationship.
5-52 0
NWC TP 6575
10009"
500
400
S300
200
LU 100 200 500 1000 1500
L" 100 (•I PERSONNEL & CARGO
LL PARACHUTES
U MISSILE MAIN RECOVERY
L, ;l PARACHUTES
U- 5
•: 4 •,•.• rM ORDNANCE PARACHUTES 40
er17 SUBSONIC MISSILE DROGUE
3• CHUTES
A Y A G S V LANDING DECELERATION 13 PARACHUTES
20 MZ SUPERSONIC MISSILE
DROGUE CHUTES
I LANDING APPROACH
•/ PARACHUTES
0.1 0.5 1.0 5.0 10 50 100
•. CANOPY LOADING W/CDS)p, PSF
FIGURE 5-47. Rate of Descent Versus Canopy Loading and Parachute Applications.
The seven application groups in Figure 5-47 can be combined into three groups in
relation to the force-reduction factor, X1. Groups I and II will have X1 factors in the 0.02- to
0.25-range (personnel and cargo) parachutes. Group III (ordnance) parachutes have X1
factors in the 0.3 to 0.7 range. These parachute groups operate at finite mass conditions. All
parachutes in Groups IV to VII have X1 factors close to or equal to 1.0 and operate at infinite
mass conditions.
5.4.6 Methods for Calculating Parachute Opening Forces
Three methods for calculating parachute opening forces are discussed in this section.
Method I, the W/(CDS)p method, is fast but should be used for preliminary calculations only.
Method 2, the Pflanz method, is mathematically exact and provides good results within certain
application limits. Method 3, the previously mentioned computerized force-trajectory-time
method, gives good results with no limitations. However, all three methods require knowledge
of certain parachute and opening-process characteristics.
0 5-53
NWC TP 6575
Method 1, W/(CDS)p Method. The equation for the parachute opening force, FX, was
defined in section 5.4.5 as
F. - (CDS)p q Cx X I
where
(CDS)p - the drag area of the full open or reefed parachute, ft2
q - the dynamic pressure at line stretch or disreef, Ib/ft2
C- - the opening-force coefficient at infinite mass, dimensionless (TIbles 5-1
through 5-5). Do not use C. at low canopy loading
X, - the force-reduction factor (the unknown factor in this equation), dimensionless
For an unreefed parachute, the drag area, (CDS)p1 of the full open parachute is used. For
a reefed parachute, a preliminary reefed drag area, (CDS),, can be calculated from the
allowable maximum parachute force, F1, and the dynamic pressure at line stretch:
(CDS)R = F
qC3 Xi
For this preliminary calculation, an opening-force coefflicient, C1, of 1.0 should be used
for the reefed parachute. The force-reduction factor, X1, can be estimated as 1.0 for reefed
drogue chutes and 0.9 for reefed main parachutes.
For the actual force calculations for unreefed parachutes, the force coefficient in
Tables 5-1 through 5-5 applies. Reefed parachutes have different opening-force coefficient
factors for the reefed and disreefed stages. Figures 5-41 and 5-42 show the drag-area-versus�time diagrams for a reefed ringsail and a reefed triconical parachute. There is no drag
overshoot for both parachutes when they open in the reefed stage. Therefore, the opening�force coefficient is 1.0. If evaluations from previous tests are not available, a C, coefficient of
1.1 should be used. For the disreef stage, the force coefficient evaluated from test data should
be used, if available; otherwise, Tables 5-1 through 5-5 will provide acceptable data.
For obtaining the opening-force reduction factor, XI, the canopy loading of the full open
or the individual reefed stages is calculated and the appropriate X1 factor as a function of
canopy loading is found in Figure 5-48.
The amount of parachute force fluctuation in the wake of the forebody must be
considered when calculating the opening force of a small drogue chute behind a large
forebody. This fluctuation is illustrated in Figure 5-49, which shows the effect of the Apollo
space capsule's wake on the opening force of the 16.5-foot-diameter ribbon drogue chute
(Reference 5.10).
5-54
NWC TP 6575
1.0o00
x 0 .8
0
. /
Ur- 0.4 /001
LU
L Dc 0.2 - - F x = (C b) S i) • • • X 1
0
o
U.
0.1
0.0
0.2 0.4 0.6 0.8 1.0 2.0 4.0 6.0 8.0 10 20 40 60 80 100
PARACHUTE CANOPY LOADING, (W/(CD S)p. PSF
FIGURE 5-48. Opening-Force Reduction Factor Versus Canopy Loading.
FORCE-TIME VEHICLE VEH:;LE
TRACE CONFIGUR - DESIGNATION DIAMETER ATION FT
BOILERPLATE 11
SJ COMMAND
MODULE
4(IP CM)
TIME
PARACHUTE $a
TEST VEHICLE
U IPTV )
TIME
INSTRUMENTED 30 CYLINDRICAL
TEST VEHICLE ( ICTV)
ex 1 09
TIME
FIGURE 5-49. Apollo Ribbon Drogue Chute
Force Fluctuation Caused by ForebodyWake
(Inflated Parachute Diameter, Dp. is 10.7 feet)
5-55
NWC TP 6575
The increase in load fluctuation from the small ICTV to the large-diameter boilerplate 0
command module (B/P CM) is apparent in the increase of the force coefficient, C1 , from 1.09 to
1.31. The force coefficient in Figure 5-49 is actually the product C, times X1, called Ck.
However, at the canopy loading of the drogue chute, X1 will be close to 1.0, approaching the
infinite mass condition.
The X1 factor can be obtained from drop tests by calculating
(CDS) q
and then plotting it versus W/(CDS)p. The data in Figure 5-48 were obtained by this method.
The X 1 factor in Figure 5-48 does not include the effect of altitude. Opening forces of
high-canopy-loading parachutes change little with altitude. However, the effect of altitude on
low-canopy-loading parachutes, such as personnel parachutes, is considerable. For
low-canopy-loading parachutes, the X, factors should be used only for altitudes below 15,000
feet. Section 5.5 contains a discussion of the altitude effect on parachute forces.
Ewing evaluated and plotted the Ck = C,,Xt factor from numerous tests of ringsail
parachutes (Reference 5.50).
French recommends plotting a Ck = C,,X 1 factor versus a mass parameter in the form
Do3/m, where Do is the nominal diameter of the parachute and m is the mass of the vehicle and
the parachute assembly (Reference 5.80).
Schilling recommends modifying this mass parameter to the form
Rm = P(CDS)p
3/ 2
mt
where mt is the total mass of vehicle plus decelerator, p is the air density, and (CDS)p is the
parachute drag area (Reference 5.81). The value p. (CDS)p3/ 2 represents the volume of the air
in and around the parachute canopy and has an obvious relationship to the apparent mass.
The altitude effect is now included in plotting Ck factors versus this mass parameter, Rm.
Figure 5-50, taken from a Northrop publication, shows Ck factors for reefed and unreefed
ribbon and ringslot parachutes plotted versus the mass parameter. These data include
supersonic deployment of ribbon parachutes.
Method 2, Pflanz Method. The Pflanz method was developed in Germany during World
War II by E. Pflanz in cooperation with the author. It was based on the following concept. A
body of known fixed weight and velocity is decelerated along a horizontal flight path by an
aerodynamic drag device whose drag area increases from a small value to 100% in a known,
mathematically definable form. This method is mathematically exact; however, no (CDS)p
overshoot is included at the start of the reefed or disreefed inflation cycle. Details of this
method may be found in References 5.76 and 5.77.
5-56 0
NWC TP 6575
16-2
Ne 1.2 AA 15212
U1.2 1.29 -0 a.
ol i I , _
II o I I i _
o w 1.34 P 2
0-1.34 .- 1.56
K3/2CS MASRTOZM C ~
LU0.80
0
MAS -KIO RM~s = C 1
Mt
S~PARACHUTE DATA
SYMBOL FOREBODY
TYPE DoFT M REEFING RATIO METHOD DEPLOY
SAPOLLO CONICAL RIBBON DROGUE 137 0308 MORTAR BUFF
SAPOLLO CONICAL RIBBON DROGUE 165 0.428 MORTAR BUFF
0 ADDPEP HEMISFLO 16.0 0.22-041 CANISTER STREAMLINED
SMERCURY CONICAL RIBBON 6.87 0.87 MORTAR STREAMLINED
SSANDIA CONICAL RIBBON 20.0 0.186 DROGUE GUN STREAMLINED
C COOK CONICAL RIBBON 844 0.20-030 PILOT CHUTE STREAMLINED
o UAR RINGSAIL 20-30 0.16-0.31 PILOT CHUTE STREAMLINED
E3 CENTURY RINGSAIL 128 0.125 PILOT CHUTE STREAMLINED
SASSET RINGSAIL 29.6 0.10'0.20 P'LOT CHUTE STREAMLINED
APOLLO BLK 1HEAVY RINGSAIL 83.5 0.08 F LOT CHUTE STREAMLINED
t APOLLO BLK I AND 7r RINGSAIL 835 0.095 PILOT CHUTE STREAMLINED
FILLED SYMBOLS INDICATE SUPERSONIC PARACHUTE DEPLOYMENT. NUMBERS ADJACENr TO DATUM
POINTS IDENTIFY MACH NO. AT PARACHUTE LINE STRETCH
FIGURE 5-50. Opening-Force Factor Versus Mass Ratio.
5-57
NWC TP 6575
A dimensionless ballistic parameter, A, is formed from known or calculated data
A=- 2Wt
(CDS)ppgVltf
where
A - ballistic parameter, dimensionless
Wt = system weight, lb
(CDS)p - parachute drag area, reefed or fully open, ft2
g = acceleration of gravity, ft/s 2
v, - velocity at line stretch or start of disreef, ft/s
p = air density at altitude of parachute inflation, slugs/ft3
tf = canopy inflation time
Wt, q. p are fixed values for each specific application, as is the drag area of the fully open
parachute, (CDS)p. A preliminary drag area of the reefed parachute, (CDS)r, can be calculated
as described in Method 1. The reefed filling time, tf,, and the canopy disreefing time, tf2, are
calculated by the method given in section 5.4.3. After calculating the ballistic parameter, A, the
force-reduction factor, X1, is obtained from Figure 5-51. However, before determining X1, the
shape of the drag area increases versus time must be determined for the selected parachute.
This drag-area-versus-time rise is denoted in Figure 5-51 by the letter n. The n = I curve is a
straight line, typical for ribbon and ringslot parachutes. The concave curve, n = 2 is
representative of solid cloth, flat circular, conical, extended-skirt, and triconical parachutes
described in section 5.4.4. The convex form of (CDS)p versus time occurs only in the reefed
inflation of extended-skirt parachutes. Refer to the comments on the C,, factor of Method I for
low-canopy-Icading, unreefej parachutes.
The Pflanz report provides extensive information on forces, time of maximum force, and
velocity decay versus time during the parachute inflation process for a variety of drag-area�versus-time increases other than those shown in Figure 5-51.
After the force factor, X1, is determined from Figure 5-51, the opening force of the
parachute is calculated as it was in Method I
Fp- (CDS)p ql(Cx)X1, lb
5-58
NWC TP 6575
1.0
0.9 n2 ..- - 1 __ _
0.8 CURVES II 0.7 _ _ _ _
X 0.5 n 1/2n 1/2
n !-' r1 '
c 0.4 -- I--1"- CD S)p n -.
0.39 ,, "" 0
0.
0O.0~~7 ,, - __ / __
• 0.06 2
0.1
Cc 0.04 n-- ~p •P "g• 1•t
0.07 F = (CD ' S~O ci C• X1 W0.05
o o 2 0 A ocO�CURVE I
SII I I1 I I 1 1 1 1 I I I I I I1 1 I I I1 1 1I I I I
I- ,
CURVE I
BALLISTIC PARAMETER, A
FIGURE 5-51. Opening-Forcc Reduction Factor, X1, Vcrsus Ballstic Parameter, A.
where
(CDS)p - the drag area of the fully open or reefed parachute
qj - the dynamic pressure at the start of inflation or at disreef
C, = the opening-force coefficient for the reefed or unreefed parachute. To be used
only for high canopy loading conditions
X1 = the force-reduction factor determined from Figure 5-51
Frequently, a velocity decay occurs between vehicle launch and canopy (line) stretch, V1.
This decay can be calculated for deceleration in a horizontal plane
V1 Vo
1+ r [ ic~s) p --g t, v.] 59
S~5-59
NWC TP 6575
where
Vo - velocity at the beginning of deceleration. All other notations are similaLr to those
previously used
The second Pflanz report (Reference 5.77) expands on the first report by determining
parachute forces and velocity versus time for straight-line trajectories of 30,60, and 90 degrees.
Ludtke, in References 5.83 and 5.84, has somewhat generalized the Pflanz method and
has included determination of parachute opening forces from deployment of any trajectory
angle.
Method 3, Force-Trajectory-Time Method. The force-trajectory-time method is a
computer approach to the parachute opening process. The recovery-system specification for
an air vehicle, drone, missile, or aircrew escape system normally defines the starting and
ending conditions of the recovery cycle, including weight of the vehicle, starting altitude.
velocity, vehicle attitude; and for final recovery or landing, the specification defines the rate of
descent at landing and the oscillation limitation. The maximum allowable parachute force is
frequently expressed in g as a multiple of the vehicle weight. A typical requirement limits the
parachute opening force to 3 to 5g, necessitating a multiple-stage recovery system consistingof
a reefed drogue chute and one or more reefed main parachutes.
These conditions require optimization of the total recovery cycle for minimum recovery
time, altitude, and range within the allowable parachute force restraints. The computer, with
its multiple-run capability that permits many variations in staging, timing, and altitude, is the
ideal tool to accomplish this task.
A force-trajectory program best meets the above requirements for calculating the vehicle
trajectory and deceleration as well as parachute forces as a function of time. The basic
approach is somewhat similar to the Pflanz method. A drag-area-versus-time profile is formed
for the total system vehicle plus decelerator. Multiple computer runs are made using the



















